
【题目】如图,将一张四边形纸片沿EF折叠,以下条件中能得出AD∥BC的条件个数是( )
①∠2=∠4:②∠2+∠3=180°;③∠1=∠6:④∠4=∠5

A.1B.2C.3D.4
【答案】D
【解析】
分别利用同旁内角互补两直线平行,同位角相等两直线平行,内错角相等两直线平行得出答案即可.
① ∵∠2=∠4,
∴AD∥BC(同位角相等两直线平行),符合题意;
②∵∠2+∠3=180°,∠5+∠3=180°,
∴∠5=∠2,
∴GF∥HE,
因为GF和HE是由DF和CE折叠得到的,
∴FD∥EC,即AD∥EC,符合题意;
③∠1=∠6,由折叠性质知∠1=∠FEC,
∴∠6=∠FEC,
∴AD∥BC,符合题意:
④由折叠的性质知, ∠GFE=∠DFE,
∴∠DFE=∠5+∠6,
∵∠6+∠DFE=180°,
∴∠5+2∠6=180°,
∵∠4=∠5,
∴∠4+2∠6=180°,
又∵∠4+2∠1=180°,
∴∠6=∠1=∠FEC,
∴AD∥BC,符合题意.

故答案为:D.


科目:初中数学 来源: 题型:
【题目】如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数是( )
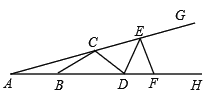
A. 80° B. 90° C. 100° D. 108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用180元购进甲种玩具的件数与用300元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共50件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1050元,商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线.求证:AD⊥BC.
(填空)

证明:∵AD是BC边上的中线
∴BD=CD(中线的意义)
在△ABD和△ACD中
∵ 
①________;②________;③________.
∴ ________≌ ________(________)
∴∠ADB=________(________)
∴∠ADB= ![]() ∠BDC=90°(平角的定义)
∠BDC=90°(平角的定义)
∴AD⊥BC(垂直的定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…分别在x轴上,点B1,B2,B3,…分别在直线y=x上,△OA1B1,△B1A1A2,△B1B2A2,△B2A2A3,△B2B3A3…,都是等腰直角三角形,如果OA1=1,则点A2019的坐标为_____.
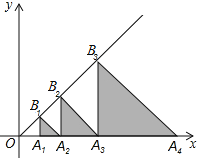
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教育科技公司销售A,B两种多媒体,这两种多媒体的进价与售价如表所示:

该教育科技公司计划购进两种多媒体共50套,共需资金132万元 .
(1)该教育科技公司计划购进A,B两种多媒体各多少套?
(2)经过市场调查后,该商店决定在原计划50套多媒体的基础上,减少A的购进数量,增加B 的购进数量,已知B种多媒体增加的数量是A种多媒体减少数量的1.5倍,全部销售后可以获取毛利润21万元,问实际购进A种多媒体多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.

(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形![]() .是否存在点P,使四边形
.是否存在点P,使四边形![]() 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将1个黑球和若干个白球入放一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球(有放回),统计数据如下表:
摸球的次数(n) | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数(m) | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率(m/n) | 0.230 | 0.207 | 0.300 | 0.260 | 0.254 |
(1)补全上表中的有关数据,并根据上表数据估计从袋中摸出一个球是黑球的概率是 ;
(2)估计口袋中白球的个数;
(3)在(2)的条件下,若小强同学有放回地连续两次摸球,用画树状图法或列表法计算他两次都摸出白球的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com