
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=![]() S△ABF,其中正确的结论有________个。
S△ABF,其中正确的结论有________个。

【答案】4
【解析】试题解析:过D作DM∥BE交AC于N,

∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴![]() ,
,
∵AE=![]() AD=
AD=![]() BC,
BC,
∴![]() ,
,
∴CF=2AF,故②正确,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=![]() BC,
BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DF=DC,故③正确;
∵tan∠CAD=![]() ,
,
而CD与AD的大小不知道,
∴tan∠CAD的值无法判断,故④错误;
∵△AEF∽△CBF,
∴![]() ,
,
∴S△AEF=![]() S△ABF,S△ABF=
S△ABF,S△ABF=![]() S矩形ABCD
S矩形ABCD
∴S△AEF=![]() S矩形ABCD,
S矩形ABCD,
又∵S四边形CDEF=S△ACD-S△AEF=![]() S矩形ABCD-
S矩形ABCD-![]() S矩形ABCD=
S矩形ABCD=![]() S矩形ABCD,
S矩形ABCD,
∴S四边形CDEF=![]() S△ABF,故⑤正确;
S△ABF,故⑤正确;
故有4个正确


科目:初中数学 来源: 题型:
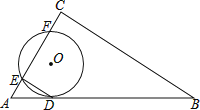
【题目】如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长度为4π.
(1)求证:DE∥BC;
(2)若AF=CE,求线段BC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD内两点M、N,满足MB⊥BC,MD⊥DC,NB⊥BA,ND⊥DA,若四边形BMDN的面积是菱形ABCD面积的![]() ,则cosA= ______ .
,则cosA= ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:

(1)方程ax2+bx+c=0的两个根为____________;
(2)不等式ax2+bx+c>0的解集为________;
(3)y随x的增大而减小的自变量x的取值范围为________;
(4)若方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(﹣2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.

(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个单位长度;
(2)△AOC与△BOD关于直线对称,则对称轴是 ;
(3)△AOC绕原点O顺时针旋转可以得到△DOB,则旋转角度是 度,在此旋转过程中,△AOC扫过的图形的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
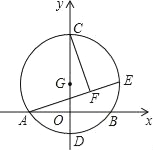
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张小卡片上分别写有数字1、2、3、4,它们除数字外没有任何区别,现将它们放在盒子里搅匀.
(1)随机地从盒子里抽取一张,求抽到数字3的概率;
(2)随机地从盒子里抽取一张,将数字记为x,不放回再抽取第二张,将数字记为y,请你用画树状图或列表的方法表示所有等可能的结果,并求出点(x,y)在函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
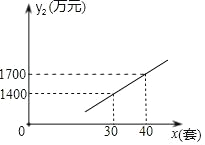
【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于80万元,已知这种设备的月产量x(套)与每套的售价y(万元)之间满足关系式y=150﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
(1)直接写出y2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com