
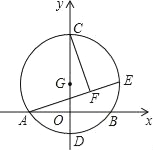
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】分析:连接AC,AG,由OG垂直于AB,利用垂径定理得到O为AB的中点,由G的坐标确定出OG的长,在直角三角形AOG中,由AG与OG的长,利用勾股定理求出AO的长,进而确定出AB的长,由CG+GO求出OC的长,在直角三角形AOC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF始终为直角三角形,点F的运动轨迹为以AC为直径的半径,如图中红线所示,当E位于点B时,CO⊥AE,此时F与O重合;当E位于D时,CA⊥AE,此时F与A重合,可得出当点E从点B出发顺时针运动到点D时,点F所经过的路径长![]() ,在直角三角形ACO中,利用锐角三角函数定义求出∠ACO的度数,进而确定出
,在直角三角形ACO中,利用锐角三角函数定义求出∠ACO的度数,进而确定出![]() 所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出
所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出![]() 的长.
的长.
详解:连接AC,AG,
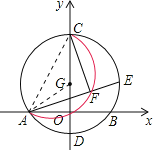
∵GO⊥AB,
∴O为AB的中点,即AO=BO=![]() AB,
AB,
∵G(0,1),即OG=1,
∴在Rt△AOG中,根据勾股定理得:AO=![]() ,
,
∴AB=2AO=2![]() ,
,
又CO=CG+GO=2+1=3,
∴在Rt△AOC中,根据勾股定理得:AC=![]() ,
,
∵CF⊥AE,
∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,
当E位于点B时,CO⊥AE,此时F与O重合;当E位于D时,CA⊥AE,此时F与A重合,
∴当点E从点B出发顺时针运动到点D时,点F所经过的路径长![]() ,
,
在Rt△ACO中,tan∠ACO=![]() ,
,
∴∠ACO=30°,
∴![]() 度数为60°,
度数为60°,
∵直径AC=2![]() ,
,
∴![]() 的长为
的长为![]() ,
,
则当点E从点B出发顺时针运动到点D时,点F所经过的路径长![]() .
.
故选B.


科目:初中数学 来源: 题型:
【题目】某市对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:A:绿化造林. B:汽车限行.C:拆除燃煤小锅炉.D:使用清洁能源.调查过程中随机抽取了部分市民进行调查,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:

(1)这次被调查的市民共有多少人?
(2)请你将统计图1补充完整;
(3)求图2中D项目对应的扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
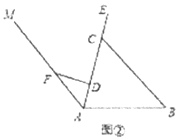
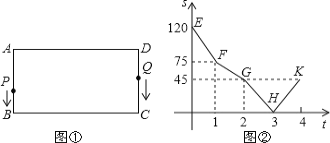
【题目】“4000辆自行车、187个服务网点”,某市区现已实现公共自行车服务全覆盖,为人们的生活带来了方便。图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A,D,C,E在同一条直线上,CD=30 cm,DF=20 cm,AF=25 cm,FD⊥AE于点D,座杆CE=15 cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
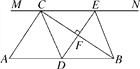
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=6,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由;
(2)在(1)的条件下,当∠A等于多少度时,四边形BECD是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
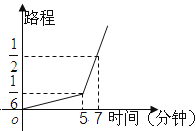
【题目】一名考生步行前往考场,5分钟走了总路程的![]() ,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示(假定总路程为1,出租车匀速),则他到达考场所花的时间比一直步行提前了________分钟。
,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示(假定总路程为1,出租车匀速),则他到达考场所花的时间比一直步行提前了________分钟。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,俄罗斯方块游戏中,图形![]() 经过平移使其填补空位,则正确的平移方式是( )
经过平移使其填补空位,则正确的平移方式是( )
[Failed to download image : http://192.168.0.10:8086/QBM/2019/8/9/2265110730670080/2266396395864065/STEM/34cd169bb880437797498d7a59a34864.png]
A.先向右平移5格,再向下平移3格
B.先向右平移4格,再向下平移5格
C.先向右平移4格,再向下平移4格
D.先向右平移3格,再向下平移5格
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,AB=30cm,BC=60cm.点P从点A出发,沿A→B→C→D路线向点D匀速运动,到达点D后停止;点Q从点D出发,沿D→C→B→A路线向点A匀速运动,到达点A后停止。若点P、Q同时出发,在运动过程中,Q点停留了1s,图②是P、Q两点在折线AB→BC→CD上相距的路程S(cm)与时间t(s)之间的函数关系图象。
(1)请解释图中点H的实际意义?
(2)求P、Q两点的运动速度;
(3)当时间t为何值时,△PCQ为等腰三角形?请直接写出t的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个整数点![]() 即各点均表示整数
即各点均表示整数![]() ,且
,且![]() ,若A、D两点表示的数的分别为
,若A、D两点表示的数的分别为![]() 和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是
和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是![]()
![]()
![]()
A. ![]() B. 0C. 1D. 2
B. 0C. 1D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )

A. 由小到大 B. 由大到小 C. 不变 D. 先由小到大,后由大到小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com