Question

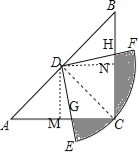
【题目】如图，在△ABC中，CA=CB，∠ACB=90°，以AB的中点D为圆心，作圆心角为90°的扇形DEF，点C恰在EF上，设∠BDF=α（0°＜α＜90°），当α由小到大变化时，图中阴影部分的面积（　　）

A. 由小到大 B. 由大到小 C. 不变 D. 先由小到大，后由大到小

Answer 1

【答案】C

【解析】试题分析：作DM⊥AC于M，DN⊥BC于N，构造正方形DMCN，利用正方形和等腰直角三角形的性质，通过证明△DMG≌△DNH，把△DHN补到△DNG的位置，得到四边形DGCH的面积=正方形DMCN的面积，于是得到阴影部分的面积=扇形的面积﹣正方形DMCN的面积，即为定值．

试题解析：解：作DM⊥AC于M，DN⊥BC于N，连接DC，

∵CA=CB，∠ACB=90°，

∴∠A=∠B=45°，

DM=AD=AB，DN=BD=AB，

∴DM=DN，

∴四边形DNCN是正方形，

∴∠MDN=90°，

∴∠MDG=90°﹣∠GDN，

∵∠EDF=90°，

∴∠NDH=90°﹣∠GDN，

∴∠MDG=∠NDH，

在△DMG和△DNH中，

，

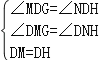∴△DMG≌△DNH，

∴四边形DGCH的面积=正方形DMCN的面积，

∵正方形DMCN的面积=DM2=AB2，

∴四边形DGCH的面积=，

∵扇形FDE的面积==，

∴阴影部分的面积=扇形面积﹣四边形DGCH的面积=（定值），

故选C．