
����Ŀ����ͼ�٣���Rt��ABC�У���C=90�㣬AB=10��BC=6����P�ӵ�A������������AB��BC���յ�C�˶�����AB����ÿ��5����λ���ȵ��ٶ��˶�����BC����ÿ��3����λ���ȵ��ٶ��˶�����Q�ӵ�C��������CA������ÿ��![]() ����λ���ȵ��ٶ��˶���P��Q����ͬʱ����������Pֹͣʱ����QҲ��ֹ֮ͣ�����P�˶���ʱ��Ϊt�룮
����λ���ȵ��ٶ��˶���P��Q����ͬʱ����������Pֹͣʱ����QҲ��ֹ֮ͣ�����P�˶���ʱ��Ϊt�룮
��1�����߶�AQ�ij������ú�t�Ĵ���ʽ��ʾ��
��2������PQ����PQ���ABC��һ��ƽ��ʱ����t��ֵ��
��3����ͼ�ڣ�����P��PE��AC�ڵ�E����PE��EQΪ�ڱ�������PEQF����DΪAC���е㣬����DF�������PEQF���ABC�ص�����ͼ�ε����ΪS��
�ٵ���Q���߶�CD���˶�ʱ����S��t֮��ĺ�����ϵʽ��
��ֱ��д��DF������PEQF�ֳ������ֵ������Ϊ1��2ʱt��ֵ��

���𰸡���1��AQ=8��![]() t��0��t��4������2��t=
t��0��t��4������2��t=![]() s��3s����3����
s��3s����3����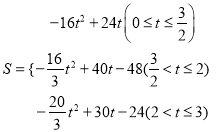 ����t=
����t=![]() s��
s��![]() s��
s��
�������������������1�����ù��ɶ��������AC������AQ=AC��CQ���ɽ�����⣻
��2�������������г�������⼴�ɣ�
��3��������������a����ͼ1�У���0��t��![]() ʱ���ص��������ı���PEQF��b����ͼ2�У���
ʱ���ص��������ı���PEQF��b����ͼ2�У���![]() ��t��2ʱ���ص��������ı���PNQE��C����ͼ3�У���2��t��3ʱ���ص������������MNPBQ���ֱ���⼴�ɣ�
��t��2ʱ���ص��������ı���PNQE��C����ͼ3�У���2��t��3ʱ���ص������������MNPBQ���ֱ���⼴�ɣ�
������������a����ͼ4�У���DE��DQ=1��2ʱ��DF������PEQF�ֳ������ֵ������Ϊ1��2��b����ͼ5�У���NE��PN=1��2ʱ��DF������PEQF�ֳ������ֵ������Ϊ1��2���ֱ��г����̼��ɽ�����⣻
����������⣺��1����Rt��ABC�У��ߡ�C=90����AB=10��BC=6����AC=![]() =
=![]() =8����CQ=
=8����CQ=![]() t����AQ=8��
t����AQ=8��![]() t��0��t��4����
t��0��t��4����
��2������PQ��BCʱ�� ![]() ����
����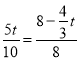 ����t=
����t=![]() s��
s��
����PQ��ABʱ�� ![]() ����
���� ����t=3��
����t=3��
����������t=![]() s��3sʱ����PQ����ABC��һ��ƽ�У�
s��3sʱ����PQ����ABC��һ��ƽ�У�
��3������ͼ1�У�a����0��t��![]() ʱ���ص��������ı���PEQF��
ʱ���ص��������ı���PEQF��
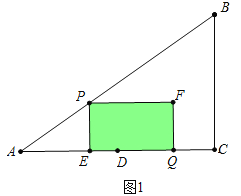
S=PEEQ=3t��8��4t��![]() t��=
t��=![]() ��
��
b����ͼ2�У���![]() ��t��2ʱ���ص��������ı���PNQE��
��t��2ʱ���ص��������ı���PNQE��
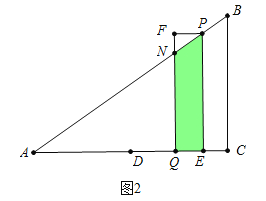
S=S�ı���PEQF��S��PFN=��16t2��24t����![]()
![]() [5t��
[5t��![]() ��8��
��8��![]() t��]
t��] ![]() [5t��
[5t��![]() ��8��
��8��![]() t0]=
t0]= ![]() ��
��
C����ͼ3�У���2��t��3ʱ���ص������������MNPBQ��
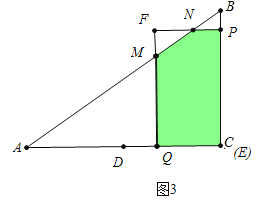
S =S�ı���PBQF -S��FNM=![]() t[6��3��t��2��]��
t[6��3��t��2��]��![]() [
[![]() t��4��t��2��]
t��4��t��2��] ![]() [
[![]() t��4��t��2��]=
t��4��t��2��]= ![]() ��
��
���������� 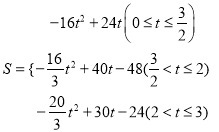 ��
��
��a����ͼ4�У���DE��DQ=1��2ʱ��DF������PEQF�ֳ������ֵ������Ϊ1��2��
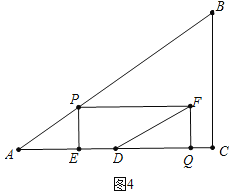
����4��4t������4��![]() t��=1��2�����t=
t��=1��2�����t=![]() s��
s��
b����ͼ5�У���NE��PN=1��2ʱ��DF������PEQF�ֳ������ֵ������Ϊ1��2��
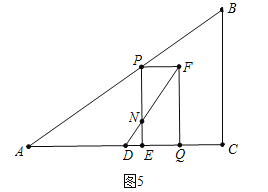
��DE��DQ=NE��FQ=1��3������4t��4������4��![]() t��=1��3�����t=
t��=1��3�����t=![]() s��
s��
������������t=![]() s��
s��![]() sʱ��DF������PEQF�ֳ������ֵ������Ϊ1��2��
sʱ��DF������PEQF�ֳ������ֵ������Ϊ1��2��


 �ο�������ϵ�д�
�ο�������ϵ�д� ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC�� ��M�ڡ�ABC�ڣ���P���߶�MC�ϣ���ABP��2��ACM.

(1)����PBC��10�㣬��BAC��80�������MPB��ֵ
(2)����M�ڵױ�BC�������ϣ���BP��AC����̽����A���ABP֮���������ϵ����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BD��AC��D��CE��AB��E��M��N�ֱ���BC��DE���е㣮
��1����֤��MN��DE��
��2����BC=20��DE=12������MDE�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���ڸ�����������������ȡ�Ա���x��һ��ֵ����x��0ʱ�����Ƕ�Ӧ�ĺ���ֵ��Ϊ�෴������x��0ʱ�����Ƕ�Ӧ�ĺ���ֵ��ȣ����dz�����������������Ϊ��غ��������磺һ�κ���y=x��1��������غ���Ϊ ��
��
��1����֪��A����5��8����һ�κ���y=ax��3����غ�����ͼ���ϣ���a��ֵ��
��2����֪���κ���![]() ��
��
�ٵ���B��m�� ![]() ���������������غ�����ͼ����ʱ����m��ֵ��
���������������غ�����ͼ����ʱ����m��ֵ��
�ڵ���3��x��3ʱ������![]() ����غ��������ֵ����Сֵ��
����غ��������ֵ����Сֵ��
��3����ƽ��ֱ������ϵ�У���M��N������ֱ�Ϊ����![]() ��1������
��1������![]() ��1}��������MN��ֱ��д���߶�MN����κ���
��1}��������MN��ֱ��д���߶�MN����κ���![]() ����غ�����ͼ��������������ʱn��ȡֵ��Χ��
����غ�����ͼ��������������ʱn��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������A��2��0��������ֱ��l1��l2�ֱ�y���ڵ�B��C�����е�B��ԭ���Ϸ�����C��ԭ���·�����֪AB=![]() ��
��
��1�����B�����ꣻ
��2������ABC�����Ϊ4����ֱ��l2�Ľ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��CEƽ����ACD��AEƽ����BAC����EAC+��ACE=90��

��1�����ж�AB��CD��λ�ù�ϵ��˵�����ɣ�
��2����ͼ2���ڣ�1���Ľ����£�����E=90�����ֲ��䣬�ƶ�ֱ�Ƕ���E��ʹ��MCE=��ECD����ֱ�Ƕ���E���ƶ�ʱ������BAE����MCD�Ƿ����ȷ����������ϵ��

��3����ͼ3���ڣ�1���Ľ����£�PΪ�߶�AC��һ���㣬��QΪֱ��CD��һ���㣬����Q������CD���˶�ʱ����C���⣩��CPQ+��CQP����BAC�к�������ϵ�� ��2��3С��ֻ��ѡһ��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������̳����ж�������ijһ��Ʒ��
��1�����̳�������Ʒ���15%����ۼ�Ϊ1.15Ԫ�������Ʒ�ڼ��̳���ԭ��Ϊ �� Ԫ��
��2�����̳�������Ʒ���20%����6ԪǮ�������Ʒ�ļ�����û���ǰ����1���������Ʒ�����̳���ԭ���Ƕ��٣�
��3���ڣ�1������2��С��������£��ס������̳��Ѹ���Ʒ����ԭ�۽��������μ۸������
���̳�����һ����۵İٷ�����![]() ���ڶ�����۵İٷ�����
���ڶ�����۵İٷ�����![]() ��
��
���̳���������۵İٷ��ʶ���![]() (
(![]() ��
��
���ʼס������̳����ĸ��̳�����۽϶ࣿ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�CA=CB����ACB=90������AB���е�DΪԲ�ģ���Բ�Ľ�Ϊ90��������DEF����Cǡ��EF�ϣ����BDF=����0�㣼����90������������С����仯ʱ��ͼ����Ӱ���ֵ������������

A. ��С���� B. �ɴ�С C. ���� D. ����С�����ɴ�С
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com