
ЁОЬтФПЁПЖЈвхЃКЖдгкИјЖЈЕФСНИіКЏЪ§ЃЌШЮШЁздБфСПxЕФвЛИіжЕЃЌЕБxЃМ0ЪБЃЌЫќУЧЖдгІЕФКЏЪ§жЕЛЅЮЊЯрЗДЪ§ЃЛЕБxЁн0ЪБЃЌЫќУЧЖдгІЕФКЏЪ§жЕЯрЕШЃЌЮвУЧГЦетбљЕФСНИіКЏЪ§ЛЅЮЊЯрЙиКЏЪ§ЃЎР§ШчЃКвЛДЮКЏЪ§y=xЉ1ЃЌЫќЕФЯрЙиКЏЪ§ЮЊ ЃЎ
ЃЎ
ЃЈ1ЃЉвбжЊЕуAЃЈЉ5ЃЌ8ЃЉдквЛДЮКЏЪ§y=axЉ3ЕФЯрЙиКЏЪ§ЕФЭМЯѓЩЯЃЌЧѓaЕФжЕЃЛ
ЃЈ2ЃЉвбжЊЖўДЮКЏЪ§![]() ЃЎ
ЃЎ
ЂйЕБЕуBЃЈmЃЌ ![]() ЃЉдкетИіКЏЪ§ЕФЯрЙиКЏЪ§ЕФЭМЯѓЩЯЪБЃЌЧѓmЕФжЕЃЛ
ЃЉдкетИіКЏЪ§ЕФЯрЙиКЏЪ§ЕФЭМЯѓЩЯЪБЃЌЧѓmЕФжЕЃЛ
ЂкЕБЉ3ЁмxЁм3ЪБЃЌЧѓКЏЪ§![]() ЕФЯрЙиКЏЪ§ЕФзюДѓжЕКЭзюаЁжЕЃЛ
ЕФЯрЙиКЏЪ§ЕФзюДѓжЕКЭзюаЁжЕЃЛ
ЃЈ3ЃЉдкЦНУцжБНЧзјБъЯЕжаЃЌЕуMЃЌNЕФзјБъЗжБ№ЮЊЃЈЉ![]() ЃЌ1ЃЉЃЌЃЈ
ЃЌ1ЃЉЃЌЃЈ![]() ЃЌ1}ЃЉЃЌСЌНсMNЃЎжБНгаДГіЯпЖЮMNгыЖўДЮКЏЪ§
ЃЌ1}ЃЉЃЌСЌНсMNЃЎжБНгаДГіЯпЖЮMNгыЖўДЮКЏЪ§![]() ЕФЯрЙиКЏЪ§ЕФЭМЯѓгаСНИіЙЋЙВЕуЪБnЕФШЁжЕЗЖЮЇЃЎ
ЕФЯрЙиКЏЪ§ЕФЭМЯѓгаСНИіЙЋЙВЕуЪБnЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ1ЃЛЃЈ2ЃЉЂйm=2Љ![]() Лђm=2+
Лђm=2+![]() Лђm=2Љ
Лђm=2Љ![]() ЃЛЂкзюДѓжЕЮЊ
ЃЛЂкзюДѓжЕЮЊ![]() ЃЌзюаЁжЕЮЊЉ
ЃЌзюаЁжЕЮЊЉ![]() ЃЛЃЈ3ЃЉЉ3ЃМnЁмЉ1Лђ1ЃМnЁм
ЃЛЃЈ3ЃЉЉ3ЃМnЁмЉ1Лђ1ЃМnЁм![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉКЏЪ§y=axЉ3ЕФЯрЙиКЏЪ§ЮЊ![]() ЃЌНЋШЛКѓНЋЕуAЃЈЉ5ЃЌ8ЃЉДњШыy=Љax+3ЧѓНтМДПЩЃЛ
ЃЌНЋШЛКѓНЋЕуAЃЈЉ5ЃЌ8ЃЉДњШыy=Љax+3ЧѓНтМДПЩЃЛ
ЃЈ2ЃЉЖўДЮКЏЪ§![]() ЕФЯрЙиКЏЪ§ЮЊ
ЕФЯрЙиКЏЪ§ЮЊ ЃЌЂйЗжЮЊmЃМ0КЭmЁн0СНжжЧщПіНЋЕуBЕФзјБъДњШыЖдгІЕФЙиЯЕЪНЧѓНтМДПЩЃЛЂкЕБЉ3ЁмxЃМ0ЪБЃЌ
ЃЌЂйЗжЮЊmЃМ0КЭmЁн0СНжжЧщПіНЋЕуBЕФзјБъДњШыЖдгІЕФЙиЯЕЪНЧѓНтМДПЩЃЛЂкЕБЉ3ЁмxЃМ0ЪБЃЌ ![]() ЃЌШЛКѓПЩ ДЫЪБЕФзюДѓжЕКЭзюаЁжЕЃЌЕБ0ЁмxЁм3ЪБЃЌКЏЪ§
ЃЌШЛКѓПЩ ДЫЪБЕФзюДѓжЕКЭзюаЁжЕЃЌЕБ0ЁмxЁм3ЪБЃЌКЏЪ§![]() ЃЌЧѓЕУДЫЪБЕФзюДѓжЕКЭзюаЁжЕЃЌДгЖјПЩЕУЕНЕБЉ3ЁмxЁм3ЪБЕФзюДѓжЕКЭзюаЁжЕЃЛ
ЃЌЧѓЕУДЫЪБЕФзюДѓжЕКЭзюаЁжЕЃЌДгЖјПЩЕУЕНЕБЉ3ЁмxЁм3ЪБЕФзюДѓжЕКЭзюаЁжЕЃЛ
ЃЈ3ЃЉЪзЯШШЗЖЈГіЖўДЮКЏЪ§![]() ЕФЯрЙиКЏЪ§гыЯпЖЮMNЧЁКУга1ИіНЛЕуЁЂ2ИіНЛЕуЁЂ3ИіНЛЕуЪБnЕФжЕЃЌШЛКѓНсКЯКЏЪ§ЭМЯѓПЩШЗЖЈГіnЕФШЁжЕЗЖЮЇЃЎ
ЕФЯрЙиКЏЪ§гыЯпЖЮMNЧЁКУга1ИіНЛЕуЁЂ2ИіНЛЕуЁЂ3ИіНЛЕуЪБnЕФжЕЃЌШЛКѓНсКЯКЏЪ§ЭМЯѓПЩШЗЖЈГіnЕФШЁжЕЗЖЮЇЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉКЏЪ§y=axЉ3ЕФЯрЙиКЏЪ§ЮЊ![]() ЃЌНЋЕуAЃЈЉ5ЃЌ8ЃЉДњШыy=Љax+3ЕУЃК5a+3=8ЃЌНтЕУЃКa=1ЃЎ
ЃЌНЋЕуAЃЈЉ5ЃЌ8ЃЉДњШыy=Љax+3ЕУЃК5a+3=8ЃЌНтЕУЃКa=1ЃЎ
ЃЈ2ЃЉЖўДЮКЏЪ§![]() ЕФЯрЙиКЏЪ§ЮЊ
ЕФЯрЙиКЏЪ§ЮЊ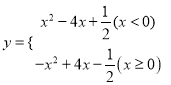 ЃЛ
ЃЛ
ЂйЕБmЃМ0ЪБЃЌНЋBЃЈmЃЌ ![]() ЃЉДњШы
ЃЉДњШы![]() ЕУ
ЕУ![]() ЃЌНтЕУЃКm=2+
ЃЌНтЕУЃКm=2+![]() ЃЈЩсШЅЃЉЛђm=2Љ
ЃЈЩсШЅЃЉЛђm=2Љ![]() ЃЎ
ЃЎ
ЕБmЁн0ЪБЃЌНЋBЃЈmЃЌ ![]() ЃЉДњШы
ЃЉДњШы![]() ЕУЃК
ЕУЃК ![]() ЃЌНтЕУЃКm=2+
ЃЌНтЕУЃКm=2+![]() Лђm=2Љ
Лђm=2Љ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃКm=2Љ![]() Лђm=2+
Лђm=2+![]() Лђm=2Љ
Лђm=2Љ![]() ЃЎ
ЃЎ
ЂкЕБЉ3ЁмxЃМ0ЪБЃЌ ![]() ЃЌХзЮяЯпЕФЖдГЦжсЮЊx=2ЃЌДЫЪБyЫцxЕФдіДѓЖјМѕаЁЃЌЁрДЫЪБyЕФзюДѓжЕЮЊ
ЃЌХзЮяЯпЕФЖдГЦжсЮЊx=2ЃЌДЫЪБyЫцxЕФдіДѓЖјМѕаЁЃЌЁрДЫЪБyЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЕБ0ЁмxЁм3ЪБЃЌКЏЪ§![]() ЃЌХзЮяЯпЕФЖдГЦжсЮЊx=2ЃЌЕБx=0газюаЁжЕЃЌзюаЁжЕЮЊЉ
ЃЌХзЮяЯпЕФЖдГЦжсЮЊx=2ЃЌЕБx=0газюаЁжЕЃЌзюаЁжЕЮЊЉ![]() ЃЌЕБx=2ЪБЃЌгазюДѓжЕЃЌзюДѓжЕy=
ЃЌЕБx=2ЪБЃЌгазюДѓжЕЃЌзюДѓжЕy=![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌЕБЉ3ЁмxЁм3ЪБЃЌКЏЪ§![]() ЕФЯрЙиКЏЪ§ЕФзюДѓжЕЮЊ
ЕФЯрЙиКЏЪ§ЕФзюДѓжЕЮЊ![]() ЃЌзюаЁжЕЮЊЉ
ЃЌзюаЁжЕЮЊЉ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ1ЫљЪОЃКЯпЖЮMNгыЖўДЮКЏЪ§![]() ЕФЯрЙиКЏЪ§ЕФЭМЯѓЧЁга1ИіЙЋЙВЕуЃЎ
ЕФЯрЙиКЏЪ§ЕФЭМЯѓЧЁга1ИіЙЋЙВЕуЃЎ
ЫљвдЕБx=2ЪБЃЌy=1ЃЌМДЉ4+8+n=1ЃЌНтЕУn=Љ3ЃЎ
ШчЭМ2ЫљЪОЃКЯпЖЮMNгыЖўДЮКЏЪ§![]() ЕФЯрЙиКЏЪ§ЕФЭМЯѓЧЁга3ИіЙЋЙВЕу
ЕФЯрЙиКЏЪ§ЕФЭМЯѓЧЁга3ИіЙЋЙВЕу

ЁпХзЮяЯп![]() гыyжсНЛЕузнзјБъЮЊ1ЃЌЁрЉn=1ЃЌНтЕУЃКn=Љ1ЃЌЁрЕБЉ3ЃМnЁмЉ1ЪБЃЌЯпЖЮMNгыЖўДЮКЏЪ§
гыyжсНЛЕузнзјБъЮЊ1ЃЌЁрЉn=1ЃЌНтЕУЃКn=Љ1ЃЌЁрЕБЉ3ЃМnЁмЉ1ЪБЃЌЯпЖЮMNгыЖўДЮКЏЪ§![]() ЕФЯрЙиКЏЪ§ЕФЭМЯѓЧЁга2ИіЙЋЙВЕуЃЎ
ЕФЯрЙиКЏЪ§ЕФЭМЯѓЧЁга2ИіЙЋЙВЕуЃЎ
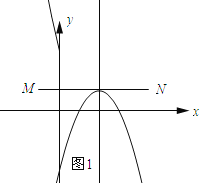
ШчЭМ3ЫљЪОЃКЯпЖЮMNгыЖўДЮКЏЪ§![]() ЕФЯрЙиКЏЪ§ЕФЭМЯѓЧЁга3ИіЙЋЙВЕуЃЎ
ЕФЯрЙиКЏЪ§ЕФЭМЯѓЧЁга3ИіЙЋЙВЕуЃЎ
ЁпХзЮяЯп![]() ОЙ§ЕуЃЈ0ЃЌ1ЃЉЃЌЁрn=1ЃЎ
ОЙ§ЕуЃЈ0ЃЌ1ЃЉЃЌЁрn=1ЃЎ
ШчЭМ4ЫљЪОЃКЯпЖЮMNгыЖўДЮКЏЪ§![]() ЕФЯрЙиКЏЪ§ЕФЭМЯѓЧЁга2ИіЙЋЙВЕуЃЎ
ЕФЯрЙиКЏЪ§ЕФЭМЯѓЧЁга2ИіЙЋЙВЕуЃЎ

ЁпХзЮяЯп![]() ОЙ§ЕуMЃЈЉ
ОЙ§ЕуMЃЈЉ![]() ЃЌ1ЃЉЃЌЁр
ЃЌ1ЃЉЃЌЁр![]() +2Љn=1ЃЌНтЕУЃКn=
+2Љn=1ЃЌНтЕУЃКn=![]() ЃЌЁр1ЃМnЁм
ЃЌЁр1ЃМnЁм![]() ЪБЃЌЯпЖЮMNгыЖўДЮКЏЪ§
ЪБЃЌЯпЖЮMNгыЖўДЮКЏЪ§![]() ЕФЯрЙиКЏЪ§ЕФЭМЯѓЧЁга2ИіЙЋЙВЕуЃЎ
ЕФЯрЙиКЏЪ§ЕФЭМЯѓЧЁга2ИіЙЋЙВЕуЃЎ
злЩЯЫљЪіЃЌnЕФШЁжЕЗЖЮЇЪЧЉ3ЃМnЁмЉ1Лђ1ЃМnЁм![]() ЃЎ
ЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШє|a|ЃНaЃЌдђгаРэЪ§aвЛЖЈТњзуЃЈЁЁЁЁЃЉ
A.aЁн0B.aЁм0C.aЃО0D.aЃМ0
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЦНУцжБНЧзјБъЯЕжаЕФШЮвтСНЕу![]() ЃЌ
ЃЌ ![]() ЃЌЮвУЧАб
ЃЌЮвУЧАб![]() Назі
Назі![]() ЁЂ
ЁЂ![]() СНЕуМфЕФЁАзЊНЧОрРыЁБЃЌМЧзї
СНЕуМфЕФЁАзЊНЧОрРыЁБЃЌМЧзї![]() ЃЎ
ЃЎ
ЃЈ1ЃЉСю![]() ЃЌOЮЊзјБъдЕуЃЌдђ
ЃЌOЮЊзјБъдЕуЃЌдђ![]() ЃН ЃЛ
ЃН ЃЛ
ЃЈ2ЃЉвбжЊOЮЊзјБъдЕуЃЌЖЏЕу![]() Тњзу
Тњзу![]() ЃЌЧыаДГіxгыyжЎМфТњзуЕФЙиЯЕЪНЃЌВЂдкЫљИјЕФжБНЧзјБъЯЕжаЃЌЛГіЫљгаЗћКЯЬѕМўЕФЕуPЫљзщГЩЕФЭМаЮЃЛ
ЃЌЧыаДГіxгыyжЎМфТњзуЕФЙиЯЕЪНЃЌВЂдкЫљИјЕФжБНЧзјБъЯЕжаЃЌЛГіЫљгаЗћКЯЬѕМўЕФЕуPЫљзщГЩЕФЭМаЮЃЛ
ЃЈ3ЃЉЩш![]() ЪЧвЛИіЖЈЕуЃЌ
ЪЧвЛИіЖЈЕуЃЌ ![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЕФЖЏЕуЃЌЮвУЧАб
ЩЯЕФЖЏЕуЃЌЮвУЧАб![]() ЕФзюаЁжЕНазі
ЕФзюаЁжЕНазі![]() ЕНжБЯп
ЕНжБЯп![]() ЕФЁАзЊНЧОрРыЁБЃЎШє
ЕФЁАзЊНЧОрРыЁБЃЎШє![]() ЕНжБЯп
ЕНжБЯп![]() ЕФЁАзЊНЧОрРыЁБЮЊ10ЃЌЧѓaЕФжЕЃЎ
ЕФЁАзЊНЧОрРыЁБЮЊ10ЃЌЧѓaЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЫЕЗЈЃКЂйЦНУцФкЃЌЙ§вЛЕугаЧвжЛгавЛЬѕжБЯпгывбжЊжБЯпДЙжБЃЛЂкЖдЖЅНЧЯрЕШЃЛЂлСНЬѕжБЯпБЛЕкШ§ЬѕжБЯпЫљНиЃЌЭЌЮЛНЧЯрЕШЃЛЂмДгжБЯпЭтвЛЕуЕНетЬѕжБЯпЕФДЙЯпЖЮНазіЕуЕНжБЯпЕФОрРыЃЌЦфжае§ШЗЕФга( )
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуPЪЧЕШБпЁїABCФквЛЕуЃЌPA=6ЃЌPB=8ЃЌPC=10ЃЌдђЁїAPCЕФУцЛ§ЪЧ__________

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌAB=10ЃЌBC=6ЃЌЕуPДгЕуAГіЗЂЃЌбиелЯпABЉBCЯђжеЕуCдЫЖЏЃЌдкABЩЯвдУПУы5ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌдкBCЩЯвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЕуQДгЕуCГіЗЂЃЌбиCAЗНЯђвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌPЃЌQСНЕуЭЌЪБГіЗЂЃЌЕБЕуPЭЃжЙЪБЃЌЕуQвВЫцжЎЭЃжЙЃЎЩшЕуPдЫЖЏЕФЪБМфЮЊtУыЃЎ
ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌPЃЌQСНЕуЭЌЪБГіЗЂЃЌЕБЕуPЭЃжЙЪБЃЌЕуQвВЫцжЎЭЃжЙЃЎЩшЕуPдЫЖЏЕФЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉЧѓЯпЖЮAQЕФГЄЃЛЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉСЌНсPQЃЌЕБPQгыЁїABCЕФвЛБпЦНааЪБЃЌЧѓtЕФжЕЃЛ
ЃЈ3ЃЉШчЭМЂкЃЌЙ§ЕуPзїPEЁЭACгкЕуEЃЌвдPEЃЌEQЮЊСкБпзїОиаЮPEQFЃЌЕуDЮЊACЕФжаЕуЃЌСЌНсDFЃЎЩшОиаЮPEQFгыЁїABCжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЎ
ЂйЕБЕуQдкЯпЖЮCDЩЯдЫЖЏЪБЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкжБНгаДГіDFНЋОиаЮPEQFЗжГЩСНВПЗжЕФУцЛ§БШЮЊ1ЃК2ЪБtЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧьзЃжаЛЊШЫУёЙВКЭЙњГЩСЂ70жмФъдФБјЪНгк2019Фъ10дТ1ШедкЬьАВУХЙуГЁТЁжиОйааЃЌДЫДЮдФБјдМ9ЭђШЫВЮгыбнСЗМАЯжГЁБЃеЯЙЄзїЃЌНЋЪ§Он9ЭђгУПЦбЇМЧЪ§ЗЈБэЪОЮЊ(ЁЁЁЁ)
A.9ЁС103B.9ЁС104C.9ЁС105D.9ЁС106
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкЁїABCжа,AD=AC,ЕуDЁЂEЁЂFЗжБ№дкBЁЂABЁЂACБпЧвBE=CF,AD+EC=AB.
(1)ЧѓжЄ:ЁїDEFЪЧЕШбќШ§НЧаЮЃЛ
(2)ЕБЁЯA=40ЁуЪБ,ЧѓЁЯDEFЕФЖШЪ§.

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com