
����Ŀ������ƽ��ֱ������ϵ�е���������![]() ��
�� ![]() �����ǰ�
�����ǰ�![]() ����
����![]() ��
��![]() �����ġ�ת�Ǿ��롱������
�����ġ�ת�Ǿ��롱������![]() ��
��
��1����![]() ��OΪ����ԭ�㣬��
��OΪ����ԭ�㣬��![]() �� ��
�� ��
��2����֪OΪ����ԭ�㣬����![]() ����
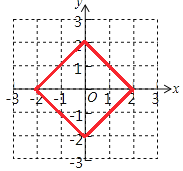
����![]() ����д��x��y֮������Ĺ�ϵʽ������������ֱ������ϵ�У��������з��������ĵ�P����ɵ�ͼ�Σ�
����д��x��y֮������Ĺ�ϵʽ������������ֱ������ϵ�У��������з��������ĵ�P����ɵ�ͼ�Σ�
��3����![]() ��һ�����㣬
��һ�����㣬 ![]() ��ֱ��
��ֱ��![]() �ϵĶ��㣬���ǰ�
�ϵĶ��㣬���ǰ�![]() ����Сֵ����
����Сֵ����![]() ��ֱ��
��ֱ��![]() �ġ�ת�Ǿ��롱����
�ġ�ת�Ǿ��롱����![]() ��ֱ��
��ֱ��![]() �ġ�ת�Ǿ��롱Ϊ10����a��ֵ��
�ġ�ת�Ǿ��롱Ϊ10����a��ֵ��

���𰸡���1��7�� ��2��![]() �� ��ͼ��������
�� ��ͼ��������
��3��a��ֵΪ4��16��
�������������������1�������¶��������⼴�ɵã�
��2�������¶���֪|x|+|y|=1���ݴ˿��Ի������������ͼ�μ��ɣ�
��3����ֱ��![]() ��һ��Q��x��x+4������d��P��Q��=|a��x|+|��2��x��4|=10�������������⼴�ɵ�.
��һ��Q��x��x+4������d��P��Q��=|a��x|+|��2��x��4|=10�������������⼴�ɵ�.
�����������1��![]() ��|3-0|+|-4-0|=3+4=7��
��|3-0|+|-4-0|=3+4=7��
�ʴ�Ϊ��7��
��2��������ã� ![]() ��
��
��ͼ������
��3����![]() ��ֱ��
��ֱ��![]() �ġ�ת�Ǿ��롱Ϊ10��
�ġ�ת�Ǿ��롱Ϊ10��
����ֱ��![]() ��һ��Q��x��x+4������d��P��Q��=10��
��һ��Q��x��x+4������d��P��Q��=10��
��|a��x|+|��2��x��4|=10����|a��x|+|x+6|=10��
��a��x��0��x�ݩ�6ʱ��ԭʽ=a��x+x+6=10�����a=4��
��a��x��0��x����6ʱ��ԭʽ=x��a��x��6=10�����a=��16��
�������ۣ�a��ֵΪ4��16��


 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������У������������( )
A.��ȵĽ��ǶԶ���
B.ͬ���ڽǻ���
C.��һ�㲻ֻ��һ��ֱ������ֱ֪�ߴ�ֱ
D.����ֱ�� a��b��c����� b��a��c��a����ô b��c
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
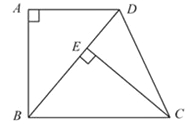
����Ŀ����ͼ����֪�ı���ABCD�����Σ�AD��BC����A��90����BC��BD��CE��BD������ΪE��
(1)��֤����ABD�ա�ECB��
(2)����DBC��50��������DCE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BD��AC��D��CE��AB��E��M��N�ֱ���BC��DE���е㣮
��1����֤��MN��DE��
��2����BC=20��DE=12������MDE�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���ڸ�����������������ȡ�Ա���x��һ��ֵ����x��0ʱ�����Ƕ�Ӧ�ĺ���ֵ��Ϊ�෴������x��0ʱ�����Ƕ�Ӧ�ĺ���ֵ��ȣ����dz�����������������Ϊ��غ��������磺һ�κ���y=x��1��������غ���Ϊ ��
��
��1����֪��A����5��8����һ�κ���y=ax��3����غ�����ͼ���ϣ���a��ֵ��
��2����֪���κ���![]() ��
��
�ٵ���B��m�� ![]() ���������������غ�����ͼ����ʱ����m��ֵ��
���������������غ�����ͼ����ʱ����m��ֵ��
�ڵ���3��x��3ʱ������![]() ����غ��������ֵ����Сֵ��
����غ��������ֵ����Сֵ��
��3����ƽ��ֱ������ϵ�У���M��N������ֱ�Ϊ����![]() ��1������
��1������![]() ��1}��������MN��ֱ��д���߶�MN����κ���
��1}��������MN��ֱ��д���߶�MN����κ���![]() ����غ�����ͼ��������������ʱn��ȡֵ��Χ��
����غ�����ͼ��������������ʱn��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��CEƽ����ACD��AEƽ����BAC����EAC+��ACE=90��

��1�����ж�AB��CD��λ�ù�ϵ��˵�����ɣ�
��2����ͼ2���ڣ�1���Ľ����£�����E=90�����ֲ��䣬�ƶ�ֱ�Ƕ���E��ʹ��MCE=��ECD����ֱ�Ƕ���E���ƶ�ʱ������BAE����MCD�Ƿ����ȷ����������ϵ��

��3����ͼ3���ڣ�1���Ľ����£�PΪ�߶�AC��һ���㣬��QΪֱ��CD��һ���㣬����Q������CD���˶�ʱ����C���⣩��CPQ+��CQP����BAC�к�������ϵ�� ��2��3С��ֻ��ѡһ��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�ķ���ֽ�У�ÿ��С�����DZ߳�Ϊ1����λ�������Σ���ABC���������㶼�ڸ���ϣ���ÿ��С����Ķ���и�㣩

��1��������ABC����ƽ��3����λ�����A1B1C1��
��2��������ABC�Ƶ�O˳ʱ����ת90�������A2B2C2�������A��ת��A2��������·�߳���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com