
【题目】已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:
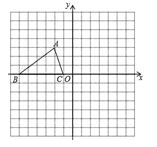
(1)A点的坐标为________;B点的坐标为________;C点的坐标为________.
(2)将点A、B、C的横坐标保持不变,纵坐标分别乘以-1,分别得点A'、B'、C',并连接A'、B'、C'得△A' B' C',请画出△A' B' C'.
(3)△A' B' C'与△ABC的位置关系是________.
【答案】(1)(-2,3),(-6,0),(-1,0);(2)答案见解析;(3)关于x轴对称
【解析】
(1)根据各点在坐标系中的位置即可得出结论,注意坐标规律(横坐标、纵坐标);
(2)把点A,B,C的横坐标保持不变,纵坐标分别乘以-1,分别得点A′,B′,C′坐标,并在图上找到各点连接A′,B′,C′得△A′B′C′即可;
(3)根据△A′B′C′与△ABC在坐标系中的位置即可得出结论,也可根据坐标关系判断,关于x轴对称横坐标不变,纵坐标互为相反数.
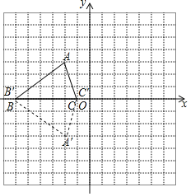
解:(1)A点的坐标为(-2,3);B点的坐标为(-6,0);C点的坐标为(-1,0);
(2)A′点的坐标为(-2, -3);B′点的坐标为(-6,0);C′点的坐标为(-1,0),如图△A′B′C′即为所求;
(3)由图可知,△A′B′C′与△ABC的位置关于x轴对称.
故答案为:关于x轴对称.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m+1)x+![]() (m2+1)=0有两个相等的实数根.
(m2+1)=0有两个相等的实数根.
(1)求m的值;
(2)将y=﹣x2+(m+1)x﹣![]() (m2+1)的图象向左平移3个单位长度,再向上平移2个单位长度,写出变化后函数的表达式;
(m2+1)的图象向左平移3个单位长度,再向上平移2个单位长度,写出变化后函数的表达式;
(3)在(2)的条件下,当直线y=2x+n与变化后的图象有公共点时,求n2﹣4n的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
新定义:
将一个平面图形分为面积相等的两部分的直线叫做该平面图形的“等积线”,其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”(例如圆的直径就是圆的“等积线段”)
解决问题:
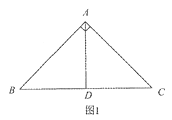
已知在Rt△ABC中,∠BAC=90°,AB=AC=2![]() .
.
(1)如图1,若AD⊥BC,垂足为D,则AD是△ABC的一条等积线段,直接写出AD的长;
(2)在图2和图3中,分别画出一条等积线段,并直接写出它们的长度. (要求:图1、图2和图3中的等积线段的长度各不相等)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户的粮食产量平均每年的增长率为![]() ,第一年的产量为50000Kg,第二年的产量为_______Kg,第三年的产量为______Kg,三年总产量为________Kg.
,第一年的产量为50000Kg,第二年的产量为_______Kg,第三年的产量为______Kg,三年总产量为________Kg.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程中,是一元二次方程共有( )
①x2﹣![]() +3=0;②2x2﹣3xy+4=0; ③x2﹣4x+k=0;④x2+mx﹣1=0;⑤3x2+x=20.
+3=0;②2x2﹣3xy+4=0; ③x2﹣4x+k=0;④x2+mx﹣1=0;⑤3x2+x=20.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四季水果店正准备促销广西“脆皮桔”和山东烟台“红富士苹果”,已知“脆皮桔”的进价为12元/千克,售价为24元/千克,“红富士苹果”的进价为10元/千克,售价为20元/千克,第一天该店销售两种水果共获利1156元,其中“脆皮桔”的销量比“红富士苹果”销量的4倍少10千克.
(1)求第一天这两种水果的销量分别是多少千克?
(2)该店在第一天的售价基础上销售一段时间后,天气突然变冷不利于“脆皮桔”的保存,为了更好的销售这两种水果,店主决定对“脆皮桔”在原来售价基础上降价a%,销量在原有基础上增加![]() a%,“红富士苹果”在原来售价基础上提升
a%,“红富士苹果”在原来售价基础上提升![]() a%,销量比原来上升了30千克,其中两种水果的进价均不变,结果每天获利比原来多300元,求a的值.
a%,销量比原来上升了30千克,其中两种水果的进价均不变,结果每天获利比原来多300元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2k+1)x+k2+1=0.
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形两邻边的长,且k=2,求该矩形的对角线L的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com