
【题目】某农户的粮食产量平均每年的增长率为![]() ,第一年的产量为50000Kg,第二年的产量为_______Kg,第三年的产量为______Kg,三年总产量为________Kg.
,第一年的产量为50000Kg,第二年的产量为_______Kg,第三年的产量为______Kg,三年总产量为________Kg.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
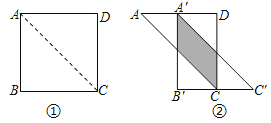
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为0.5cm2,则它移动的距离AA′等于( )
A.![]() cmB.
cmB.![]() cmC.
cmC.![]() cm或
cm或![]() cmD.
cmD.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的一个交点
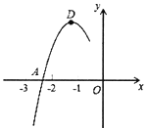
轴的一个交点![]() 在点(-3, 0)和(-2 ,0)之间,其部分图象如图,则以下结论:①
在点(-3, 0)和(-2 ,0)之间,其部分图象如图,则以下结论:①![]() <0;②
<0;②![]() <0;③
<0;③![]() =2;④方程
=2;④方程![]() 有两个相等的实数根,其中正确结论的个数为________个.
有两个相等的实数根,其中正确结论的个数为________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:
若b′=![]() ,则称点Q为点P的理想点.例如:点(1,2)的理想点的坐标是(1,﹣2),点(﹣2,3)的理想点的坐标是(﹣2,3).
,则称点Q为点P的理想点.例如:点(1,2)的理想点的坐标是(1,﹣2),点(﹣2,3)的理想点的坐标是(﹣2,3).
(1)点(![]() ,﹣1)理想点的坐标是_____;若点C在函数y=2x2的图象上,则它的理想点是A(1,﹣2),B(﹣1,2)中的哪一个?_____;
,﹣1)理想点的坐标是_____;若点C在函数y=2x2的图象上,则它的理想点是A(1,﹣2),B(﹣1,2)中的哪一个?_____;
(2)若点P在函数y=﹣2x+4(﹣2≤x≤k,k>﹣2)的图象上,其理想点为Q:
①若其理想点Q的纵坐标b′的取值范围是﹣6≤b′≤10,求k的值;
②在①的条件下,若点P的理想点Q都不在反比例函数y=![]() (m<0,x>0)上,求m的取值范围.
(m<0,x>0)上,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生甲与乙学习概率初步知识后设计了如下游戏:甲手中有 ![]() 、
、![]() 、
、![]() 三张扑克牌,乙手中有
三张扑克牌,乙手中有 ![]() 、
、![]() 、
、![]() 三张扑克牌,每局比赛时,两人从各自手中随机取一张牌进行比较,数字大的则本局获胜.
三张扑克牌,每局比赛时,两人从各自手中随机取一张牌进行比较,数字大的则本局获胜.
(1)若每人随机取出手中的一张牌进行比较,请列举出所有情况;
(2)求学生乙一局比赛获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:
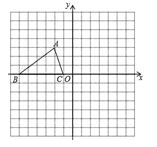
(1)A点的坐标为________;B点的坐标为________;C点的坐标为________.
(2)将点A、B、C的横坐标保持不变,纵坐标分别乘以-1,分别得点A'、B'、C',并连接A'、B'、C'得△A' B' C',请画出△A' B' C'.
(3)△A' B' C'与△ABC的位置关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).
(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD
面上的概率为0.75;若存在,指出其中的一种平移方式;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
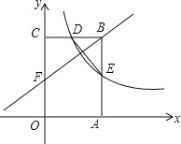
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),反比例函数y=![]() (k>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(k>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求反比例函数的表达式及点E的坐标;
(2)点F是OC边上一点,若△FBC∽△DEB,求点F的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com