
【题目】如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?

【答案】50海里
【解析】
试题过点A作AD⊥BC于D,则垂线段AD的长度为与钓鱼岛A最近的距离,线段CD的长度即为所求.先由方位角的定义得出∠ABC=30°,∠ACD=60°,由三角形外角的性质得出∠BAC=30°,则CA=CB=100海里,然后解直角△ADC,得出CD=![]() AC=50海里。
AC=50海里。
解:过点A作AD⊥BC于D,
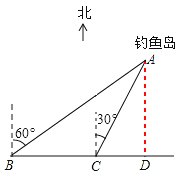
根据题意得,∠ABC=30°,∠ACD=60°,
∴∠BAC=∠ACD﹣∠ABC=30°。∴CA=CB。
∵CB=50×2=100(海里),∴CA=100(海里)。
在Rt△ADC中,∠ACD=60°,∴CD=![]() AC=
AC=![]() ×100=50(海里)。
×100=50(海里)。
故船继续航行50海里与钓鱼岛A的距离最近。


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)请求出抛物线的解析式;
(2)当0<x<4时,请直接写出y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )

A. π-4 B. ![]() π-1 C. π-2 D.
π-1 C. π-2 D. ![]() -2
-2
【答案】C
【解析】试题解析:∵∠BAC=45°,
∴∠BOC=90°,
∴△OBC是等腰直角三角形,
∵OB=2,
∴△OBC的BC边上的高为:![]() OB=
OB=![]() ,
,
∴BC=2![]()
∴S阴影=S扇形OBC﹣S△OBC=![]() .
.
故选C.
【题型】单选题
【结束】
10
【题目】夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )

A.8m B.6.4m C.4.8m D.10m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生甲与乙学习概率初步知识后设计了如下游戏:甲手中有 ![]() 、
、![]() 、
、![]() 三张扑克牌,乙手中有
三张扑克牌,乙手中有 ![]() 、
、![]() 、
、![]() 三张扑克牌,每局比赛时,两人从各自手中随机取一张牌进行比较,数字大的则本局获胜.
三张扑克牌,每局比赛时,两人从各自手中随机取一张牌进行比较,数字大的则本局获胜.
(1)若每人随机取出手中的一张牌进行比较,请列举出所有情况;
(2)求学生乙一局比赛获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 ,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:
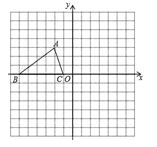
(1)A点的坐标为________;B点的坐标为________;C点的坐标为________.
(2)将点A、B、C的横坐标保持不变,纵坐标分别乘以-1,分别得点A'、B'、C',并连接A'、B'、C'得△A' B' C',请画出△A' B' C'.
(3)△A' B' C'与△ABC的位置关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(3k+1)x+2k2+2k=0.
(1)求证:无论k取何实数值,方程总有实数根;
(2)若等腰△ABC的一边长a=6,另两边长b、c恰好是这个方程的两个根,求此三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
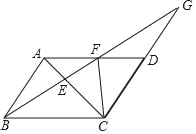
【题目】如图,AC是ABCD的对角线,在AD边上取一点F,连接BF交AC于点E,并延长BF交CD的延长线于点G.
(1)若∠ABF=∠ACF,求证:CE2=EFEG;
(2)若DG=DC,BE=6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
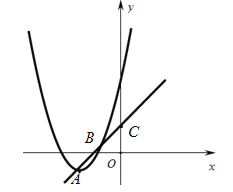
【题目】如图,二次函数与一次函数交于顶点![]() 和点
和点![]() 两点,一次函数与
两点,一次函数与![]() 轴交于点
轴交于点![]() .
.
(1)求二次函数![]() 和一次函数
和一次函数![]() 的解析式;
的解析式;
(2)![]() 轴上存在点
轴上存在点![]() 使
使![]() 的面积为9,求点
的面积为9,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com