
【题目】已知关于x的一元二次方程x2-(3k+1)x+2k2+2k=0.
(1)求证:无论k取何实数值,方程总有实数根;
(2)若等腰△ABC的一边长a=6,另两边长b、c恰好是这个方程的两个根,求此三角形的周长.
【答案】(1)证明见解析;(2)△ABC的周长为16或22.
【解析】
(1)计算方程的判别式大于等于0即可;
(2)由等腰三角形的性质有a=b=6、a=c=6或b=c三种情况,当b=6或c=6时,可知x=2为方程的一个根,代入可求得k的值,则可求得方程的根,可求得三边长;当b=c时,可知方程有两个相等的实数根,由判别式等于0可求得k,同样可求得方程的两根,可求得三角形的三边长和周长.
(1)∵![]() =b2-4ac=[-(3k+1)]2-4(2k2+2k)=9k2+6k+1-8k2-8k=k2-2k+1=(k-1)2≥0,
=b2-4ac=[-(3k+1)]2-4(2k2+2k)=9k2+6k+1-8k2-8k=k2-2k+1=(k-1)2≥0,
∴无论k取何值,方程总有实数根.
(2)①若a=6为底边,则b,c为腰长,则b=c,则△=0.
∴(k-1)2=0,解得k=1.
此时原方程化为x2-4x+4=0.
∴x1=x2=2,即b=c=2.
此时△ABC三边为6,2,2不能构成三角形.
②若a=b为腰,则b,c中一边为腰,不妨设b=a=6,
代入方程:62-6(3k+1)+2k2+2k=0,
解得k=3或5.
则原方程化为x2-10x+24=0,或x2-16x+60=0.
解得x1=4,x2=6;或x1=6,x2=10.
所以b=6,c=4;或b=6,c=10.
此时△ABC三边为6,6,4或6,6,10能构成三角形,
所以△ABC的周长为6+6+4=16,或6+6+10=22.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
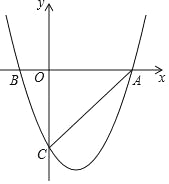
【题目】如图,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于C点,连接AC,A(3,0),AC=3![]() .
.
(1)求抛物线的函数解析式,并直接写出顶点坐标;
(2)点P是第四象限内抛物线上一点,过点P作PQ⊥AC于Q,直接写出当线段PQ长度最大时,点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)该二次函数图象的对称轴是;
(2)若该二次函数的图象开口向上,当![]() 时,函数图象的最高点为
时,函数图象的最高点为![]() ,最低点为
,最低点为![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,求点
,求点![]() 和点
和点![]() 的坐标;
的坐标;
(3)对于该二次函数图象上的两点![]() ,
,![]() ,设
,设![]() ,当
,当![]() 时,均有
时,均有![]() ,请结合图象,直接写出
,请结合图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方
向依次不断移动,每次移动1个单位,其行走路线如下图所示.

(1)填写下列各点的坐标:A4( , )、A8( , )、A12( , );
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A100到点A101的移动方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板如图甲放置,其中![]() ,
,![]() ,
,![]() ,斜边
,斜边![]() ,
,![]() .把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点
.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点![]() ,与D1E1相交于点F.
,与D1E1相交于点F.
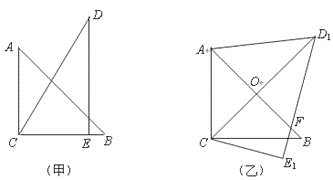
(1)求![]() 的度数;
的度数;
(2)求线段AD1的长;
(3)若把三角形D1CE1绕着点![]() 顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由.
顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com