
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 ,为什么?

【答案】⑴围成矩形长为30m,宽为25 m时,能使矩形面积为750㎡。
⑵不能。
【解析】
试题(1)设所围矩形ABCD的长AB为x米,则宽AD为![]() 米,根据矩形面积的计算方法列出方程求解;(2)假使矩形面积为810米,则方程无实数根,所以不能围成矩形场地.
米,根据矩形面积的计算方法列出方程求解;(2)假使矩形面积为810米,则方程无实数根,所以不能围成矩形场地.
试题解析:(1)设所围矩形ABCD的长AB为x米,则宽AD为![]() 米.
米.
依题意,得![]() ,即
,即![]() .
.
解此方程,得x1=30,x2=50.
∵墙的长度不超过45m,∴x2=50不合题意,应舍去.
当x=30时,![]() .
.
答:当所围矩形的长为30m、宽为25m时,能使矩形的面积为750m2.
(2)不能.理由如下:
由![]() 得
得![]() .
.
∵![]() ,
,
∴方程![]() 没有实数根.
没有实数根.
∴不能使所围矩形场地的面积为810m2.


科目:初中数学 来源: 题型:
【题目】某公交车每月的支出费用为4000元,票价为2元/人,设每月有![]() 人乘坐该公交车,每月利润为
人乘坐该公交车,每月利润为![]() 元(利润=收入-支出).
元(利润=收入-支出).
(1)请写出![]() 与
与![]() 的关系式 ;
的关系式 ;
(2)完成表格.
| 500 | 1000 | 1500 | 2000 | 2500 | 3000 | … |
|
|
|
|
|
|
| … |
(3)观察表中数据,每月乘客量达到 人以上时,该公交车才不会亏损.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=y1-y2,y1与x成反比例,y2与x-2成正比例,并且当x=3时,y=5;当x=1时,y=-1.
(1)y与x的函数表达式;(2)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程的解法中,错误的个数是( )
①方程2x-1=x+1移项,得3x=0
②方程![]() =1去分母,得x-1=3=x=4
=1去分母,得x-1=3=x=4
③方程1-![]() 去分母,得4-x-2=2(x-1)
去分母,得4-x-2=2(x-1)
④方程![]() 去分母,得2x-2+10-5x=1
去分母,得2x-2+10-5x=1
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
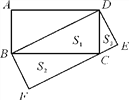
【题目】如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1__ __S2+S3;(填“>”“=”或“<”)
(2)写出图中的三对相似三角形,并选择其中一对进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的解析式为y=2x+5,其图象过点A(-2,a),B(b,-1).
(1)求a,b的值,并画出此一次函数的图象;
(2)在y轴上是否存在点C,使得AC+BC的值最小?若存在,求出点C的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是菱形ABCD的对角线AC上一动点,过P作垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,则△AMN的面积为y,则y关于x的函数图象的大致形状是( )

A. 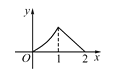 B.
B. 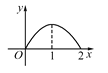
C. 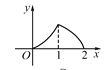 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
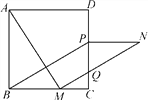
【题目】如图,在正方形ABCD中,点M是BC边上的任一点,连结AM并将线段AM绕点M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连结NP、BP.
(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连结AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司有A型、B型、C型三种型号的电脑,其中A型每台2500元、B型每台4000元、C型每台6000元,某中学现有资金100500元,计划全部用于从这家电脑公司购进36台两种型号的电脑这,这个学校有哪几种购买方案可选择,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com