
【题目】已知y=y1-y2,y1与x成反比例,y2与x-2成正比例,并且当x=3时,y=5;当x=1时,y=-1.
(1)y与x的函数表达式;(2)当![]() 时,求
时,求![]() 的值.
的值.
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】在第九章中我们研究了几种特殊四边形,请根据你的研究经验来自己研究一种特殊四边形——筝形.
初识定义:两组邻边分别相等的四边形是筝形.
(1)根据筝形的定义,写出一种你学过的四边形满足筝形的定义的是 .
性质研究:
(2)类比你学过的特殊四边形的性质,通过观察、测量、折叠、证明等操作活动,对如图的筝形ABCD(AB=AD,BC=CD)的性质进行探究,以下判断正确的有 (填序号).
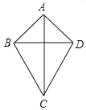
①AC⊥BD;②AC、BD互相平分;
③AC平分∠BAD和∠BCD;
④∠ABC=∠ADC;⑤∠BAD+∠BCD=180°;
⑥筝形ABCD的面积为![]() AC×BD.
AC×BD.
(3)在上面的筝形性质中选择一个进行证明.
性质应用:
(4)直接利用你发现的筝形的性质解决下面的问题:
如图,在筝形ABCD中,AB=BC,AD=CD,点P是对角线BD上一点,过P分别做AD、CD垂线,垂足分别为点M、N.当筝形ABCD满足条件 时,四边形PNDM是正方形?请说明理由.
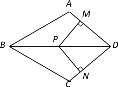
判定方法:
(5)回忆我们学习过的特殊四边形的判定方法(如四边相等的四边形是菱形),用文字语言写出筝形的一个判定方法(除定义外): .
查看答案和解析>>
科目:初中数学 来源: 题型:
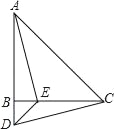
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠ACD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春平中学要为学校科技活动小组提供实验器材,计划购买A型、B型两种型号的放大镜.若购买8个A型放大镜和5个B型放大镜需用220元;若购买4个A型放大镜和6个B型放大镜需用152元.
(1)求每个A型放大镜和每个B型放大镜各多少元;
(2)春平中学决定购买A型放大镜和B型放大镜共75个,总费用不超过1180元,那么最多可以购买多少个A型放大镜?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着夏季的到来,我县居民的用电量猛增.目前,我县城市居民用电收费方式有以下两种:
①普通电价付费方式:全天0.52元/度;
②峰谷电价付费方式:用电高峰时段(早8:00—晚21:00)0.65元/度;
用电低谷时段(晚21:00—早8:00)0.40元/度.
(1)已知小丽家5月份总用电量为280度.
①若其中高峰时段用电量为80度,则小丽家按照哪种方式付电费比较合算?能省多少元?
②若小丽家采用峰谷电价付费方式交电费137元,那么,小丽家高峰时段用电量为多少度?
(2)到6月份付费时,小丽发现6月份总用电量为320度,用峰谷电价付费方式比普通电价付费方式省了18.4元,那么,6月份小丽家高峰时段用电量为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生带手机上学的现象越来越受到社会的关注.某市记者随机调查了一些家长对这种现象的态度(A:无所谓;B:反对;C:赞成),并将调査结果绘制成图①和图②的统计图(不完整).
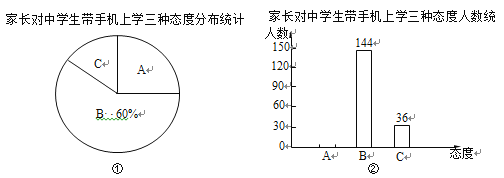
请根据图中提供的信息,解答下列问题:
(1)在图①中,C部分所占扇形的圆心角度数为___________°;选择图①进行统计的优点是___________;
(2)将图②补充完整;
(3)根据抽样调查结果,可估计该市50000名中学生家长中有_________名家长持赞成态度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 ,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com