
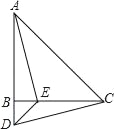
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠ACD的度数.
【答案】(1)证明见解析;(2)60°
【解析】试题分析:(1)利用SAS即可得证;
(2)由全等三角形对应角相等得到∠AEB=∠CDB,利用外角的性质求出∠AEB的度数,即可确定出∠BDC的度数,进而利用三角形的内角和得出∠ACD的度数.
试题解析:
(1)证明:在△ABE和△CBD中,
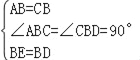 ,
,
∴△ABE≌△CBD(SAS);
(2)∵在△ABC中,AB=CB,∠ABC=90°,
∴∠BAC=∠ACB=45°,
由(1)得:△ABE≌△CBD,
∴∠AEB=∠BDC,
∵∠AEB为△AEC的外角,
∴∠AEB=∠ACB+∠CAE=30°+45°=75°,
∴∠BDC=75°.
∴∠ACD=180°﹣∠BAC﹣∠BDC=180°﹣45°﹣75°=60°.


科目:初中数学 来源: 题型:
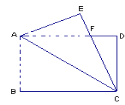
【题目】如图,在长方形ABCD中,将△ABC沿AC对折至△AEC位置,CE与AD交于点F.
(1)试说明:AF=FC;(2)如果AB=12,BC=16,求AF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交车每月的支出费用为4000元,票价为2元/人,设每月有![]() 人乘坐该公交车,每月利润为
人乘坐该公交车,每月利润为![]() 元(利润=收入-支出).
元(利润=收入-支出).
(1)请写出![]() 与
与![]() 的关系式 ;
的关系式 ;
(2)完成表格.
| 500 | 1000 | 1500 | 2000 | 2500 | 3000 | … |
|
|
|
|
|
|
| … |
(3)观察表中数据,每月乘客量达到 人以上时,该公交车才不会亏损.
查看答案和解析>>
科目:初中数学 来源: 题型:
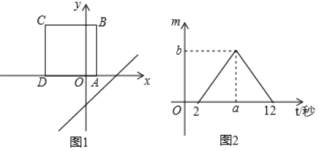
【题目】如图1,将正方形ABCD置于平面直角坐标系中,其中AD边在x轴上,其余各边均与坐标轴平行,直线l:y=x﹣3沿x轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中b的值为( )
A. 5![]() B. 4
B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
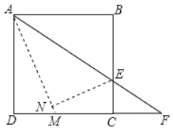
【题目】如图,正方形ABCD的边长为8,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,当AB=2CF时,则NM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3)。双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE。
的图像经过BC的中点D,且与AB交于点E,连接DE。

(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=y1-y2,y1与x成反比例,y2与x-2成正比例,并且当x=3时,y=5;当x=1时,y=-1.
(1)y与x的函数表达式;(2)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是菱形ABCD的对角线AC上一动点,过P作垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,则△AMN的面积为y,则y关于x的函数图象的大致形状是( )

A. 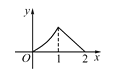 B.
B. 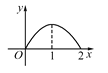
C. 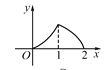 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com