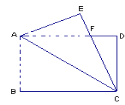
【题目】如图，在长方形ABCD中，将△ABC沿AC对折至△AEC位置，CE与AD交于点F.
（1）试说明：AF=FC；（2）如果AB=12，BC=16，求AF的长
期末金牌卷系列答案
轻松课堂标准练系列答案科目：初中数学 来源： 题型：
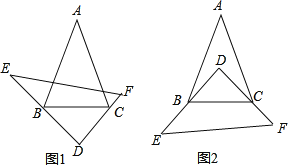
【题目】已知：在△ABC和△DEF中，∠A=40°，∠E+∠F=100°，将△DEF如图摆放，使得∠D的两条边分别经过点B和点C．
（1）当将△DEF如图1摆放时，则∠ABD+∠ACD= 度；
（2）当将△DEF如图2摆放时，请求出∠ABD+∠ACD的度数，并说明理由．
（3）能否将△DE摆放到某个位置时，使得BD、CD同时平分∠ABC和∠ACB？直接写出结论 （填“能”或“不能”）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在四边形ABCD中，AB∥CD，∠ABC=90°，动点P从A点出发，沿A→D→C→B匀速运动，设点P运动的路程为x，△ABP的面积为y，图象如图2所示.
⑴①AD= , CD= , BC= ; （填空）
②当点P运动的路程x=8时，△ABP的面积为y= ; （填空）
⑵求四边形ABCD的面积
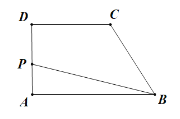
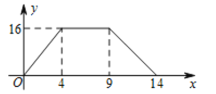
图1 图2
查看答案和解析>>
科目：初中数学 来源： 题型：
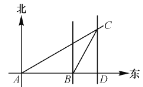
【题目】如图，已知某船于上午8点在A处观测小岛C在北偏东60°方向上.该船以每小时30海里的速度向东航行到B处，此时测得小岛C在北偏东30°方向上.船以原速度再继续向东航行1.5小时到达小岛C的正南方D点.求船从A到D一共走了多少海里？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是抛物线y＝ax2＋bx＋c(a≠0)的部分图象，其顶点坐标为(1，n)，抛物线与x轴的一个交点在点(3，0)和(4，0)之间．则下列结论
①a－b＋c＞0；②3a＋b＝0；
③b2＝4a(c－n)；
④一元二次方程ax2＋bx＋c＝n－1有两个不相等的实数根．
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在第九章中我们研究了几种特殊四边形，请根据你的研究经验来自己研究一种特殊四边形——筝形．
初识定义：两组邻边分别相等的四边形是筝形．
（1）根据筝形的定义，写出一种你学过的四边形满足筝形的定义的是 ．
性质研究：
（2）类比你学过的特殊四边形的性质，通过观察、测量、折叠、证明等操作活动，对如图的筝形ABCD（AB＝AD，BC＝CD）的性质进行探究，以下判断正确的有 （填序号）．
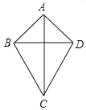
①AC⊥BD；②AC、BD互相平分；
③AC平分∠BAD和∠BCD；
④∠ABC＝∠ADC；⑤∠BAD＋∠BCD＝180°；
⑥筝形ABCD的面积为
AC×BD．
（3）在上面的筝形性质中选择一个进行证明．
性质应用：
（4）直接利用你发现的筝形的性质解决下面的问题：
如图，在筝形ABCD中，AB＝BC，AD＝CD，点P是对角线BD上一点，过P分别做AD、CD垂线，垂足分别为点M、N．当筝形ABCD满足条件 时，四边形PNDM是正方形？请说明理由．
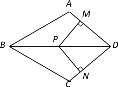
判定方法：
（5）回忆我们学习过的特殊四边形的判定方法（如四边相等的四边形是菱形），用文字语言写出筝形的一个判定方法（除定义外）： ．
查看答案和解析>>
科目：初中数学 来源： 题型：
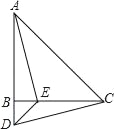
【题目】如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连接AE、DE、DC．
（1）求证：△ABE≌△CBD；
（2）若∠CAE=30°，求∠ACD的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
