
ЁОЬтФПЁПвбжЊЃКдкЁїABCКЭЁїDEFжаЃЌЁЯA=40ЁуЃЌЁЯE+ЁЯF=100ЁуЃЌНЋЁїDEFШчЭМАкЗХЃЌЪЙЕУЁЯDЕФСНЬѕБпЗжБ№ОЙ§ЕуBКЭЕуCЃЎ
ЃЈ1ЃЉЕБНЋЁїDEFШчЭМ1АкЗХЪБЃЌдђЁЯABD+ЁЯACD= ЖШЃЛ
ЃЈ2ЃЉЕБНЋЁїDEFШчЭМ2АкЗХЪБЃЌЧыЧѓГіЁЯABD+ЁЯACDЕФЖШЪ§ЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉФмЗёНЋЁїDEАкЗХЕНФГИіЮЛжУЪБЃЌЪЙЕУBDЁЂCDЭЌЪБЦНЗжЁЯABCКЭЁЯACBЃПжБНгаДГіНсТл ЃЈЬюЁАФмЁБЛђЁАВЛФмЁБЃЉ
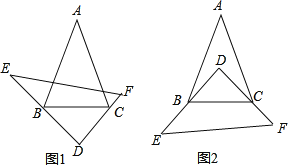
ЁОД№АИЁПЃЈ1ЃЉ240ЃЛЃЈ2ЃЉ30ЁуЃЛЃЈ3ЃЉВЛФм.
ЁОНтЮіЁП
ЃЈ1ЃЉвЊЧѓЁЯABD+ЁЯACDЕФЖШЪ§ЃЌжЛвЊЧѓГіЁЯABC+ЁЯCBD+ЁЯACB+ЁЯBCDЃЌРћгУШ§НЧаЮФкНЧКЭЖЈРэЕУГіЁЯABC+ЁЯACB=180Ёу-ЁЯA=180Ёу-40Ёу=140ЁуЃЛИљОнШ§НЧаЮФкНЧКЭЖЈРэЃЌЁЯCBD+ЁЯBCD=ЁЯE+ЁЯF=100ЁуЃЌЕУГіЁЯABD+ЁЯACD=ЁЯABC+ЁЯCBD+ЁЯACB+ЁЯBCD=140Ёу+100Ёу=240ЁуЃЛ
ЃЈ2ЃЉвЊЧѓЁЯABD+ЁЯACDЕФЖШЪ§ЃЌжЛвЊЧѓГіЁЯABC+ЁЯACB-ЃЈЁЯBCD+ЁЯCBDЃЉЕФЖШЪ§ЃЎИљОнШ§НЧаЮФкНЧКЭЖЈРэЃЌЁЯCBD+ЁЯBCD=ЁЯE+ЁЯF=100ЁуЃЛИљОнШ§НЧаЮФкНЧКЭЖЈРэЕУЃЌЁЯABC+ЁЯACB=180Ёу-ЁЯA=140ЁуЃЌЕУГіЁЯABD+ЁЯACD=ЁЯABC+ЁЯACB-ЃЈЁЯBCD+ЁЯCBDЃЉ=140Ёу-100Ёу=40ЁуЃЛ
ЃЈ3ЃЉВЛФмЃЎМйЩшФмНЋЁїDEFАкЗХЕНФГИіЮЛжУЪБЃЌЪЙЕУBDЁЂCDЭЌЪБЦНЗжЁЯABCКЭЁЯACBЃЎдђЁЯCBD+ЁЯBCD=ЁЯABD+ЁЯACD=100ЁуЃЌФЧУДЁЯABC+ЁЯACB=200ЁуЃЌгыШ§НЧаЮФкНЧКЭЖЈРэУЌЖмЃЌЫљвдВЛФмЃЎ
ЃЈ1ЃЉдкЁїABCжаЃЌЁЯA+ЁЯABC+ЁЯACB=180ЁуЃЌЁЯA=40Ёу
ЁрЁЯABC+ЁЯACB=180Ёу-ЁЯA=180Ёу-40Ёу=140Ёу
дкЁїBCDжаЃЌЁЯD+ЁЯBCD+ЁЯCBD=180Ёу
ЁрЁЯBCD+ЁЯCBD=180Ёу-ЁЯD
дкЁїDEFжаЃЌЁЯD+ЁЯE+ЁЯF=180Ёу
ЁрЁЯE+ЁЯF=180Ёу-ЁЯD
ЁрЁЯCBD+ЁЯBCD=ЁЯE+ЁЯF=100Ёу
ЁрЁЯABD+ЁЯACD=ЁЯABC+ЁЯCBD+ЁЯACB+ЁЯBCD=140Ёу+100Ёу=240ЁуЃЌ
ЙЪД№АИЮЊ240ЃЎ
ЃЈ2ЃЉЁЯABD+ЁЯACD=30ЁуЃЛ
РэгЩШчЯТЃК
ЁпЁЯE+ЁЯF=100Ёу
ЁрЁЯD=180Ёу-ЃЈЁЯE+ЁЯFЃЉ=80Ёу
ЁрЁЯABD+ЁЯACD=180Ёу-ЁЯA-ЁЯDBC-ЁЯDCB
=180Ёу-50Ёу-ЃЈ180Ёу-80ЁуЃЉ
=30ЁуЃЛ
ЃЈ3ЃЉВЛФмЃЎМйЩшФмНЋЁїDEFАкЗХЕНФГИіЮЛжУЪБЃЌЪЙЕУBDЁЂCDЭЌЪБЦНЗжЁЯABCКЭЁЯACBЃЎдђЁЯCBD+ЁЯBCD=ЁЯABD+ЁЯACD=100ЁуЃЌФЧУДЁЯABC+ЁЯACB=200ЁуЃЌгыШ§НЧаЮФкНЧКЭЖЈРэУЌЖмЃЌ
ЙЪД№АИЮЊЃКВЛФмЃЎ


 вЛХЕЪщвЕЪюМйзївЕПьРжМйЦкдЦФЯУРЪѕГіАцЩчЯЕСаД№АИ
вЛХЕЪщвЕЪюМйзївЕПьРжМйЦкдЦФЯУРЪѕГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃК
ЃЈ1ЃЉ![]()
ЃЈ2ЃЉаЁУїНтВЛЕШЪН![]() Ём1ЕФЙ§ГЬШчЯТЃЌЧыжИГіЫћНтД№Й§ГЬжаПЊЪМГіЯжДэЮѓВНжшЕФађКХЃЌВЂаДГіе§ШЗЕФНтД№Й§ГЬЃЎ
Ём1ЕФЙ§ГЬШчЯТЃЌЧыжИГіЫћНтД№Й§ГЬжаПЊЪМГіЯжДэЮѓВНжшЕФађКХЃЌВЂаДГіе§ШЗЕФНтД№Й§ГЬЃЎ
НтЃКШЅЗжФИЕУЃК3ЃЈ1+xЃЉЉ2ЃЈ2x+1ЃЉЁм1ЁЁЂй
ШЅРЈКХЕУЃК3+3xЉ4x+1Ём1ЁЁЂк
вЦЯюЕУЃК3xЉ4xЁм1Љ3Љ1ЁЁЂл
КЯВЂЭЌРрЯюЕУЃКЉxЁмЉ3ЁЁЂм
СНБпЖМГ§вдЉ1ЕУЃКxЁм3ЁЁЂн
НтЃКПЊЪМГіЯжДэЮѓЕФВНжшађКХЮЊЁЁ ЃЌе§ШЗЕФНтД№Й§ГЬЁЁ ЃЎ
ЃЈ3ЃЉвбжЊЪЕЪ§xЃЌyТњзуЗНГЬзщ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЦНЗНИљЃЛ
ЕФЦНЗНИљЃЛ
ЃЈ4ЃЉЧѓВЛЕШЪНзщ ЕФећЪ§НтЃЎ
ЕФећЪ§НтЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
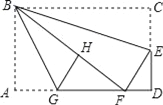
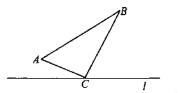
ЁОЬтФПЁПШчЭМЃЌдкОиаЮжНЦЌABCDжаЃЌAB=6ЃЌBC=10ЃЌЕуEдкCDЩЯЃЌНЋЁїBCEбиBEелЕўЃЌЕуCЧЁТфдкБпADЩЯЕФЕуFДІЃЛЕуGдкAFЩЯЃЌНЋЁїABGбиBGелЕўЃЌЕуAЧЁТфдкЯпЖЮBFЩЯЕФЕуHДІЃЌгаЯТСаНсТлЃК
ЂйЁЯEBG=45ЁуЃЛЂкЁїDEFЁзЁїABGЃЛЂлSЁїABG=![]() SЁїFGHЃЛЂмAG+DF=FGЃЎ
SЁїFGHЃЛЂмAG+DF=FGЃЎ
Цфжае§ШЗЕФЪЧ__ЃЎЃЈАбЫљгае§ШЗНсТлЕФађКХЖМбЁЩЯЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбРтГЄЮЊ1cmЕФШєИЩИіаЁе§ЗНЬхАкЗХШчЭМЫљЪОЕФМИКЮЬхЃЌШЛКѓдкТЖГіЕФБэУцЩЯЭПЩЯбеЩЋ![]() ВЛКЌЕзУц
ВЛКЌЕзУц![]()
![]() ИУМИКЮЬхжагаЖрЩйаЁе§ЗНЬхЃП
ИУМИКЮЬхжагаЖрЩйаЁе§ЗНЬхЃП
![]() ЛГіжїЪгЭМЃЎ
ЛГіжїЪгЭМЃЎ
![]() ЧѓГіЭПЩЯбеЩЋВПЗжЕФзмУцЛ§ЃЎ
ЧѓГіЭПЩЯбеЩЋВПЗжЕФзмУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
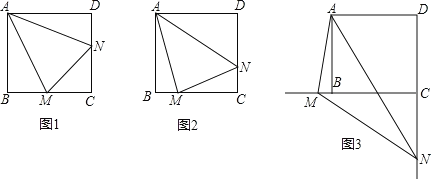
ЁОЬтФПЁПвбжЊЃКе§ЗНаЮABCDжаЃЌЁЯMAN=45ЁуЃЌЁЯMANШЦЕуAЫГЪБеыа§зЊЃЌЫќЕФСНБпЗжБ№НЛCBЁЂDCЃЈЛђЫќУЧЕФбгГЄЯпЃЉгкЕуMЁЂNЃЎЕБЁЯMANШЦЕуAа§зЊЕНBM=DNЪБЃЈШчЭМЃЉЃЌвзжЄBM+DN=MNЃЎ
ЃЈ1ЃЉЕБЁЯMANШЦЕуAа§зЊЕНBMЁйDNЪБЃЈШчЭМЃЉЃЌЯпЖЮBMЁЂDNКЭMNжЎМфгадѕбљЕФЪ§СПЙиЯЕЃПаДГіВТЯыЃЌВЂМгвджЄУїЃЛ
ЃЈ2ЃЉЕБЁЯMANШЦЕуAа§зЊЕНШчЭМЕФЮЛжУЪБЃЌЯпЖЮBMЁЂDNКЭMNжЎМфгжгадѕбљЕФЪ§СПЙиЯЕЃПЧыжБНгаДГіФуЕФВТЯыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЎЕу
ЃЎЕу![]() ДгЕу
ДгЕу![]() ГіЗЂби
ГіЗЂби![]() ТЗОЖЯђжеЕу
ТЗОЖЯђжеЕу![]() дЫЖЏЃЛЕу
дЫЖЏЃЛЕу![]() Дг
Дг![]() ЕуГіЗЂби
ЕуГіЗЂби![]() ТЗОЖЯђжеЕу
ТЗОЖЯђжеЕу![]() дЫЖЏЃЎЕу
дЫЖЏЃЎЕу![]() КЭ
КЭ![]() ЗжБ№вд1КЭ3ЕФдЫЖЏЫйЖШЭЌЪБПЊЪМдЫЖЏЃЌСНЕуЖМвЊЕНЯргІЕФжеЕуЪБВХФмЭЃжЙдЫЖЏЃЌдкФГЪБПЬЃЌЗжБ№Й§
ЗжБ№вд1КЭ3ЕФдЫЖЏЫйЖШЭЌЪБПЊЪМдЫЖЏЃЌСНЕуЖМвЊЕНЯргІЕФжеЕуЪБВХФмЭЃжЙдЫЖЏЃЌдкФГЪБПЬЃЌЗжБ№Й§![]() КЭ
КЭ![]() зї
зї![]() гк
гк![]() ЃЌ
ЃЌ![]() гк
гк![]() ЃЎдђЕу
ЃЎдђЕу![]() дЫЖЏЪБМфЕШгк____________ЪБЃЌ
дЫЖЏЪБМфЕШгк____________ЪБЃЌ![]() гы
гы![]() ШЋЕШЁЃ
ШЋЕШЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуPЕФзјБъЮЊЃЈx1ЃЌy1ЃЉЃЌЕуQЕФзјБъЮЊЃЈx2ЃЌy2ЃЉЃЌЧвx1Ёйx2ЃЌy1Ёйy2ЃЎШєPЃЌQЮЊФГИіОиаЮЕФСНИіЖЅЕуЃЌЧвИУОиаЮЕФБпОљгыФГЬѕзјБъжсДЙжБЃЌдђГЦИУОиаЮЮЊЕуPЃЌQЕФЁАЯрЙиОиаЮЁБЃЌЯТЭМЂйЮЊЕуPЃЌQЕФЁАЯрЙиОиаЮЁБЕФЪОвтЭМЃЎ

вбжЊЕуAЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌ
ЃЈ1ЃЉШєЕуBЕФзјБъЮЊЃЈ3ЃЌ1ЃЉЃЌЧѓЕуAЃЌBЕФЁАЯрЙиОиаЮЁБЕФУцЛ§ЃЛ
ЃЈ2ЃЉЕуCдкжБЯпxЃН3ЩЯЃЌШєЕуAЃЌCЕФЁАЯрЙиОиаЮЁБЮЊе§ЗНаЮЃЌЧѓжБЯпACЕФБэДяЪНЃЛ
ЃЈ3ЃЉШєЕуDЕФзјБъЮЊЃЈ4ЃЌ2ЃЉЃЌНЋжБЯпyЃН2x+bЦНвЦЃЌЕБЫќгыЕуAЃЌDЕФЁАЯрЙиОиаЮЁБУЛгаЙЋЙВЕуЪБЃЌЧѓГіbЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЙ§ЦНааЫФБпаЮABCDЖдНЧЯпНЛЕуOЕФжБЯпНЛADгкEЃЌНЛBCгкFЃЌШєAB=5ЃЌBC=6ЃЌOE=2ЃЌФЧУДЫФБпаЮEFCDжмГЄЪЧЃЈЁЁЁЁЃЉ
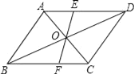
A. 16B. 15C. 14D. 13
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
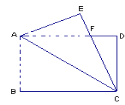
ЁОЬтФПЁПШчЭМЃЌдкГЄЗНаЮABCDжаЃЌНЋЁїABCбиACЖделжСЁїAECЮЛжУЃЌCEгыADНЛгкЕуF.
ЃЈ1ЃЉЪдЫЕУїЃКAF=FCЃЛЃЈ2ЃЉШчЙћAB=12ЃЌBC=16ЃЌЧѓAFЕФГЄ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com