
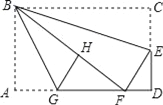
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=![]() S△FGH;④AG+DF=FG.
S△FGH;④AG+DF=FG.
其中正确的是__.(把所有正确结论的序号都选上)
【答案】①③④
【解析】试题解析:∵△BCE沿BE折叠,点C恰落在边AD上的点F处,
∴∠1=∠2,CE=FE,BF=BC=10,
在Rt△ABF中,∵AB=6,BF=10,
∴AF=![]() =8,
=8,
∴DF=AD-AF=10-8=2,
设EF=x,则CE=x,DE=CD-CE=6-x,
在Rt△DEF中,∵DE2+DF2=EF2,
∴(6-x)2+22=x2,解得x=![]() ,
,
∴ED= ![]() ,
,
∵△ABG沿BG折叠,点A恰落在线段BF上的点H处,
∴∠3=∠4,BH=BA=6,AG=HG,
∴∠2+∠3=![]() ∠ABC=45°,所以①正确;
∠ABC=45°,所以①正确;

HF=BF-BH=10-6=4,
设AG=y,则GH=y,GF=8-y,
在Rt△HGF中,∵GH2+HF2=GF2,
∴y2+42=(8-y)2,解得y=3,
∴AG=GH=3,GF=5,
∵∠A=∠D,![]() ,
,![]() ,
,
∴![]() ,
,
∴△ABG与△DEF不相似,所以②错误;
∵S△ABG=![]() 63=9,S△FGH=
63=9,S△FGH=![]() GHHF=
GHHF=![]() ×3×4=6,
×3×4=6,
∴S△ABG=![]() S△FGH,所以③正确;
S△FGH,所以③正确;
∵AG+DF=3+2=5,而GF=5,
∴AG+DF=GF,所以④正确.
∴①③④正确.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
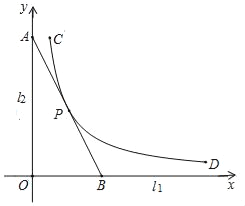
【题目】如图,直线l1,l2是紧靠某湖泊的两条相互垂直的公路,曲线段CD是该湖泊环湖观光大道的一部分.现准备修建一条直线型公路AB,用以连接两条公路和环湖观光大道,且直线AB与曲线段CD有且仅有一个公共点P.已知点C到l1,l2的距离分别为8km和1km,点P到l1的距离为4km,点D到l1的距离为0.8km.若分别以l1,l2为x轴、y轴建立平面直角坐标系xOy,则曲线段CD对应的函数解析式为y=![]() .
.
(1)求k的值,并指出函数y=![]() 的自变量的取值范围;
的自变量的取值范围;
(2)求直线AB的解析式,并求出公路AB长度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上.有四位同学分别测量出以下4组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B两点之间距离的有( )
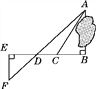
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P、Q分别从点A、B同时开始移动,点P的速度为1 cm/秒,点Q的速度为2 cm/秒,点Q移动到点C后停止,点P也随之停止运动下列时间瞬间中,能使△PBQ的面积为15cm 的是( )
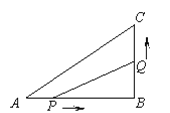
A. 2秒钟 B. 3秒钟 C. 4秒钟 D. 5秒钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
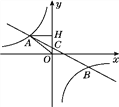
【题目】【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话。
⑴现有1,2,3,4,5,6,7,8,9共九个数字,请将它们分别填入图1的九个方格中,使得每行的三个数、每列的三个数、斜对角的三个数之和都等于15.
⑵通过研究问题⑴,利用你发现的规律,将3,5,-7,1,7,-3,9,-5,-1
这九个数字分别填入图2的九个方格中,使得横、竖、斜对角的所有三个数的和都相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
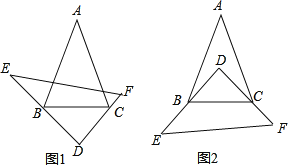
【题目】已知:在△ABC和△DEF中,∠A=40°,∠E+∠F=100°,将△DEF如图摆放,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,则∠ABD+∠ACD= 度;
(2)当将△DEF如图2摆放时,请求出∠ABD+∠ACD的度数,并说明理由.
(3)能否将△DE摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB?直接写出结论 (填“能”或“不能”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com