
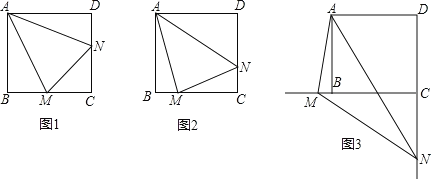
����Ŀ����֪��������ABCD�У���MAN=45�㣬��MAN�Ƶ�A˳ʱ����ת���������߷ֱ�CB��DC�������ǵ��ӳ��ߣ��ڵ�M��N������MAN�Ƶ�A��ת��BM=DNʱ����ͼ������֤BM+DN=MN��
��1������MAN�Ƶ�A��ת��BM��DNʱ����ͼ�����߶�BM��DN��MN֮����������������ϵ��д�����룬������֤����
��2������MAN�Ƶ�A��ת����ͼ��λ��ʱ���߶�BM��DN��MN֮������������������ϵ����ֱ��д����IJ��룮
���𰸡�(1)������;(2)������.
��������
��1���ֱ�֤����ABE�ա�ADN����AEM�ա�ANM������ȫ�������ε����ʽ��
��2���ɣ�1����֤��������ͬ��֤�����ɣ�
��1�����룺BM+DN=MN��֤�����£�
��ͼ2����MB���ӳ����ϣ���ȡBE=DN������AE��
�ڡ�ABE�͡�ADN�У���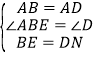 �����ABE�ա�ADN��SAS������AE=AN����EAB=��NAD��
�����ABE�ա�ADN��SAS������AE=AN����EAB=��NAD��
�ߡ�BAD=90�㣬��MAN=45�㣬���BAM+��DAN=45�㣬���EAB+��BAM=45�㣬���EAM=��NAM��
�ڡ�AEM�͡�ANM�У���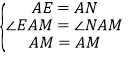 �����AEM�ա�ANM��SAS������ME=MN����ME=BE+BM=BM+DN����BM+DN=MN��
�����AEM�ա�ANM��SAS������ME=MN����ME=BE+BM=BM+DN����BM+DN=MN��
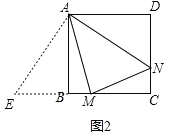
��2��DN=MN+BM��֤�����£�
��ͼ3����DC�Ͻ�ȡDF=BM������AF��
�ڡ�ABM�͡�ADF�У���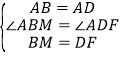 �����ABM�ա�ADF��SAS������AM=AF����BAM=��DAF�����BAM+��BAF=��BAF+��DAF=90�㣬����MAF=��BAD=90�㣮
�����ABM�ա�ADF��SAS������AM=AF����BAM=��DAF�����BAM+��BAF=��BAF+��DAF=90�㣬����MAF=��BAD=90�㣮
�ߡ�MAN=45�㣬���MAN=��FAN=45�㣮
�ڡ�MAN�͡�FAN�У���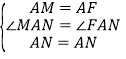 �����MAN�ա�FAN��SAS������MN=NF����MN=DN��DF=DN��BM����DN��BM=MN����DN=MN+BM��
�����MAN�ա�FAN��SAS������MN=NF����MN=DN��DF=DN��BM����DN��BM=MN����DN=MN+BM��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������������У�ÿ��С�����εı߳���Ϊ1����λ�� ![]() ���������㶼�ڸ���ϣ�
���������㶼�ڸ���ϣ�
��1���������л���![]() ����ƽ��3����λ�õ���
����ƽ��3����λ�õ���![]() ��
��
��2���������л���![]() ����ֱ��
����ֱ��![]() �ԳƵ�
�ԳƵ�![]() ��
��
��3����ֱ��![]() �ϻ�һ��
�ϻ�һ��![]() ��ʹ��
��ʹ��![]() ��ֵ���
��ֵ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ץס��ɽ�Ļ������ڵ��̻���ij�̵��������A��B���������ڼ���Ʒ��������A�ּ���Ʒ8����B�ּ���Ʒ3������Ҫ950Ԫ��������A�ּ���Ʒ5����B�ּ���Ʒ6������Ҫ800Ԫ��
��1����A��B���ּ���Ʒÿ���������Ԫ��
��2�������̵�������������ּ���Ʒ��100���������г�������ʽ���ת�����ڹ�����100������Ʒ���ʽ�����7500Ԫ����������7650Ԫ����ô���̵깲�м��ֽ���������
��3��������ÿ��A�ּ���Ʒ�ɻ�����20Ԫ��ÿ��B�ּ���Ʒ�ɻ�����30Ԫ���ڵڣ�2���ʵĸ��ֽ��������У���һ�ַ������������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ź�ͼ����˵��Զ��ʱ������е�һ����걳�ϵ�ͼ�������ֳơ��걳ͼ�����й��Ŵ���ѧʷ�Ͼ����о���һ��
������1��2��3��4��5��6��7��8��9���Ÿ����֣��뽫���Ƿֱ�����ͼ1�ľŸ������У�ʹ��ÿ�е���������ÿ�е���������б�Խǵ�������֮�Ͷ�����15��
��ͨ���о�����ţ������㷢�ֵĹ��ɣ���3��5����7��1��7����3��9����5����1
��Ÿ����ֱַ�����ͼ2�ľŸ������У�ʹ�úᡢ����б�Խǵ������������ĺͶ���ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���а����¹涨��ȡÿ�µ�ˮ�ѣ���ˮ������7�֣���ÿ��1.5Ԫ�շѣ�������7�֣�δ����������ÿ��1.5Ԫ��ȡ��������������ÿ��2.3Ԫ�շѣ�
��1�����ij�û�5�·�ˮ��ƽ��Ϊÿ��1.6Ԫ����ô���û�5�·�Ӧ��ˮ�Ѷ���Ԫ��
��2�����ij�û�5�·ݽ�ˮ��17.4Ԫ����ô���û�5�·�ˮ��ƽ��ÿ�ֶ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABC����DEF�У���A=40������E+��F=100��������DEF��ͼ�ڷţ�ʹ�á�D�������߷ֱ���B�͵�C��
��1��������DEF��ͼ1�ڷ�ʱ�����ABD+��ACD= �ȣ�
��2��������DEF��ͼ2�ڷ�ʱ���������ABD+��ACD�Ķ�������˵�����ɣ�
��3���ܷ���DE�ڷŵ�ij��λ��ʱ��ʹ��BD��CDͬʱƽ�֡�ABC�͡�ACB��ֱ��д������ ����������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��D��BC�ߵ��е㣬��E��F�ֱ���AD�����ӳ����ϣ���CE��BF������BE��CF��
��1����֤���ı���EBFC�����Σ�
��2����BD��4��BE��5�����ı���EBFC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B�ֱ�������OM��ON���˶��������O�غϣ���
��1����ͼ1������MON=90������OBA����OAB��ƽ���߽��ڵ�C�����ACB= ����
��2����ͼ2������MON=n������OBA����OAB��ƽ���߽��ڵ�C�����ACB�Ķ�����
��3����ͼ2������MON=n������AOB����ǡ�ABN����BAM��ƽ���߽��ڵ�D�����ACB���ADB֮���������ϵ���������ADB�Ķ�����
��4����ͼ3������MON=80����BC�ǡ�ABN��ƽ���ߣ�BC�ķ����ӳ������OAB��ƽ���߽��ڵ�E�����ʣ����ŵ�A��B���˶�����E�Ĵ�С�����������ᣬ���E�Ķ���������ᣬ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ij��������8����A���۲�С��C�ڱ�ƫ��60�㷽����.�ô���ÿСʱ30������ٶ����е�B������ʱ���С��C�ڱ�ƫ��30�㷽����.����ԭ�ٶ��ټ�������1.5Сʱ����С��C�����Ϸ�D��.��A��Dһ�����˶��ٺ��
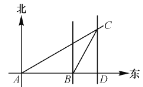
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com