
【题目】如图,点A、B分别在射线OM、ON上运动(不与点O重合).
(1)如图1,若∠MON=90°,∠OBA、∠OAB的平分线交于点C,则∠ACB= °;
(2)如图2,若∠MON=n°,∠OBA、∠OAB的平分线交于点C,求∠ACB的度数;
(3)如图2,若∠MON=n°,△AOB的外角∠ABN、∠BAM的平分线交于点D,求∠ACB与∠ADB之间的数量关系,并求出∠ADB的度数;
(4)如图3,若∠MON=80°,BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点E.试问:随着点A、B的运动,∠E的大小会变吗?如果不会,求∠E的度数;如果会,请说明理由.
【答案】(1)135;(2)90°+![]() n°;(3)90°-
n°;(3)90°-![]() n°;(4)40°
n°;(4)40°
【解析】
(1)由三角形内角和定理得出∠OBA+∠OAB=90°,由角平分线的也得出∠ABC+∠BAC=![]() ×90°=45°,再由三角形内角和定理即可得出结果;
×90°=45°,再由三角形内角和定理即可得出结果;
(2)由三角形内角和定理和角平分线的也得出∠ABC+∠BAC=90°-![]() n°,再由三角形内角和定理得出∠ACB的度数;
n°,再由三角形内角和定理得出∠ACB的度数;
(3)求出∠CBD=90°,同理∠CAD=90°,由四边形内角和求出∠ACB+∠ADB=180°,由(1)知:∠ACB=90°+![]() n°,即可得出结果;
n°,即可得出结果;
(4)由三角形外角性质得出∠OAB=∠NBA-∠AOB,由角平分线定义得出![]() ∠NBA=∠E+
∠NBA=∠E+![]() ∠OAB,
∠OAB,![]() ∠NBA=∠E+
∠NBA=∠E+![]() (∠NBA-80°),
(∠NBA-80°),![]() ∠NBA=∠E+
∠NBA=∠E+![]() ∠NBA-40°,即可得出结果.
∠NBA-40°,即可得出结果.
(1)∵∠MON=90°,
∴∠OBA+∠OAB=90°,
∵∠OBA、∠OAB的平分线交于点C,
∴∠ABC+∠BAC=![]() ×90°=45°,
×90°=45°,
∴∠ACB=180°-45°=135°;
故答案为:135;
(2)在△AOB中,∠OBA+∠OAB=180°-∠AOB=180°-n°,
∵∠OBA、∠OAB的平分线交于点C,
∴∠ABC+∠BAC=![]() (∠OBA+∠OAB)=
(∠OBA+∠OAB)=![]() (180°-n°),
(180°-n°),
即∠ABC+∠BAC=90°-![]() n°,
n°,
∴∠ACB=180°-(∠ABC+∠BAC)=180°-(90°-![]() n°)=90°+
n°)=90°+![]() n°;
n°;
(3)∵BC、BD分别是∠OBA和∠NBA的角平分线,
∴∠ABC=![]() ∠OBA,∠ABD=
∠OBA,∠ABD=![]() ∠NBA,
∠NBA,
∠ABC+∠ABD=![]() ∠OBA+
∠OBA+![]() ∠NBA,∠ABC+∠ABD=
∠NBA,∠ABC+∠ABD=![]() (∠OBA+∠NBA)=90°,
(∠OBA+∠NBA)=90°,
即∠CBD=90°,
同理:∠CAD=90°,
∵四边形内角和等于360°,
∴∠ACB+∠ADB=360°-90°-90°=180°,
由(1)知:∠ACB=90°+![]() n°,
n°,
∴∠ADB=180°-(90°+![]() n°)=90°-
n°)=90°-![]() n°,
n°,
∴∠ACB+∠ADB=180°,∠ADB=90°-![]() n°;
n°;
(4)∠E的度数不变,∠E=40°;理由如下:
∵∠NBA=∠AOB+∠OAB,
∴∠OAB=∠NBA-∠AOB,
∵AE、BC分别是∠OAB和∠NBA的角平分线,
∴∠BAE=![]() ∠OAB,∠CBA=
∠OAB,∠CBA=![]() ∠NBA,
∠NBA,
∠CBA=∠E+∠BAE,即![]() ∠NBA=∠E+
∠NBA=∠E+![]() ∠OAB,
∠OAB,
![]() ∠NBA=∠E+
∠NBA=∠E+![]() (∠NBA-80°),
(∠NBA-80°),
![]() ∠NBA=∠E+
∠NBA=∠E+![]() ∠NBA-40°,
∠NBA-40°,
∴∠E=40°.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
某中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地校参加社会实践活动.设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量 | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
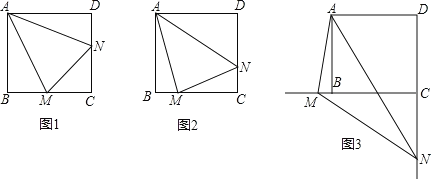
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.当∠MAN绕点A旋转到BM=DN时(如图),易证BM+DN=MN.
(1)当∠MAN绕点A旋转到BM≠DN时(如图),线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;
(2)当∠MAN绕点A旋转到如图的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,下图①为点P,Q的“相关矩形”的示意图.

已知点A的坐标为(1,0),
(1)若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
(2)点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(3)若点D的坐标为(4,2),将直线y=2x+b平移,当它与点A,D的“相关矩形”没有公共点时,求出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动__秒时,以P、Q、E、F为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过平行四边形ABCD对角线交点O的直线交AD于E,交BC于F,若AB=5,BC=6,OE=2,那么四边形EFCD周长是( )
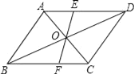
A. 16B. 15C. 14D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
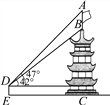
【题目】如图,某建筑物BC顶部有一旗杆AB,且点A、B、C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果保留小数后一位).(参考数据:tan47°≈1.07,tan42°≈0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场有一种游戏,规则是:在一只装有8个红球和若干个白球(每个球除颜色外都相同)的不透明的箱子中,随机摸出1个球,摸到红球就可获得一瓶饮料.工作人员统计了参加游戏的人数和获得饮料的人数(见下表).
(1)计算并完成表格;
参加游戏的人数 | 200 | 300 | 400 | 500 |
获得饮料的人数 | 39 | 63 | 82 | 99 |
获得饮料的频率 |
(2)估计获得饮料的概率;
(3)请你估计袋中白球的数量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com