
【题目】如果点P(2x+6,x-4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
试题根据平面直角坐标系中各象限点的特征,判断其所在象限,四个象限的符号特征分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-)。因此,
由点P(2x+6,x-4)在平面直角坐标系的第四象限内,得![]() 。
。
解一元一次不等式组,先求出不等式组中每一个不等式的解集,再利用口诀求出这些解集的公共部分:同大取大,同小取小,大小小大中间找,大大小小解不了(无解)。因此,![]() 。
。
不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个。在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示。故选C。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为提倡低碳环保,某公司决定购买10台节省能源的新机器,现有甲、乙两种型号的机器可选,其中每台的价格、产量如下表:
甲型机器 | 乙型机器 | |
价格(万元/台) | a | b |
产量(吨/月) | 240 | 180 |
经调查:购买一台甲型机器比购买一台乙型机器多12万元,购买2台甲型机器比购买3台乙型机器多6万元.
(1) 求a、b的值;
(2) 若该公司购买新机器的资金不超过216万元,请问该公司有哪几种购买方案?
(3) 在(2)的条件下,若公司要求每月的产量不低于1890吨,请你为该公司设计一 种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A,B,C的坐标分别为(a,0),(2,﹣4),(c,0),且a,c满足方程![]() 为二元一次方程.
为二元一次方程.
(1)求A,C的坐标.
(2)若点D为y轴正半轴上的一个动点.
①如图1,∠AOD+∠ADO+∠DAO=180°,当AD∥BC时,∠ADO与∠ACB的平分线交于点P,求∠P的度数;
②如图2,连接BD,交x轴于点E.若S△ADE≤S△BCE成立.设动点D的坐标为(0,d),求d的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共180件,其进价和售价如表:(注:获利=售价-进价)
甲 | 乙 | |
进价(元/件) | 14 | 35 |
售价(元/件) | 20 | 43 |
(1)若商店计划销售完这批商品后能获利1240元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于5040元,且销售完这批商品后获利多于1312元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
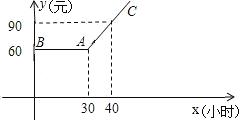
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,点
,点![]() 、
、![]() 分别是直线
分别是直线![]() 、
、![]() 上的两点.将射线
上的两点.将射线![]() 绕点
绕点![]() 顺时针匀速旋转,将射线
顺时针匀速旋转,将射线![]() 绕点
绕点![]() 顺时针匀速旋转,旋转后的射线分别记为
顺时针匀速旋转,旋转后的射线分别记为![]() 、
、![]() ,已知射线
,已知射线![]() 、射线
、射线![]() 旋转的速度之和为6度/秒.
旋转的速度之和为6度/秒.

(1)射线![]() 先转动
先转动![]() 得到射线
得到射线![]() ,然后射线
,然后射线![]() 、
、![]() 再同时旋转10秒,此时射线
再同时旋转10秒,此时射线![]() 与射线
与射线![]() 第一次出现平行.求射线
第一次出现平行.求射线![]() 、
、![]() 的旋转速度;
的旋转速度;
(2)若射线![]() 、
、![]() 分别以(1)中速度同时转动
分别以(1)中速度同时转动![]() 秒,在射线
秒,在射线![]() 与射线
与射线![]() 重合之前,设射线
重合之前,设射线![]() 与射线
与射线![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,如图2所示.
,如图2所示.
①当![]() 时,求
时,求![]() 、
、![]() 、
、![]() 满足的数量关系;
满足的数量关系;
②当![]() 时,求
时,求![]() 和
和![]() 满足的数量关系.
满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图:

(1)如图甲,以点O为中心,把点P顺时针旋转45°;
(2)如图乙,以点O为中心,把线段AB逆时针旋转90°;
(3)如图丙,以点O为中心,把△ABC顺时针旋转120°;
(4)如图丁,以点B为中心,把△ABC旋转180°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com