Question

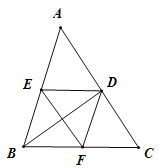
【题目】已知，如图，平分交于点，点、分别是、的中点，连接，且.

(1) 求证:；

(2)连接，若，，求四边形的面积.

Answer 1

【答案】（1）见解析；（2）6

【解析】

（1）由平行线的性质和角平分线的概念可得BE=DE，易证四边形DEFC是平行四边形，可得DE=CF，等量代换即可得出结论；

（2）易证四边形BEDF是平行四边形，再由BE=DE证得四边形BEDF是菱形，由等腰三角形“三线合一”可得BD⊥EF，根据勾股定理求得BD，根据三角形中位线定理求得EF，根据菱形的面积公式即可得出答案.

（1）证明：∵DE∥BC，

∴∠DBC=∠BDE，

∵BD平分∠ABC，

∴∠EBD=∠DBC，

∴∠BDE=∠EBD，

∴BE=DE，

∵E、F是AB、BC的中点，

∴EF∥AC，

∵DE∥BC，

∴四边形DEFC是平行四边形，

∴DE=CF，

∴BE=CF；

（2）∵AB=BC=5，BD平分∠ABC，

∴BD⊥AC，CD=AC=3.

在Rt△BDC中，

BD==4.

∵E、F是AB、BC的中点，

∴EF=AC=3.

∵F是BC中点，

∴BF=CF，

∴DE=BF，DE∥BF，

∴四边形BEDF是平行四边形，

又∵BE=DE，

∴四边形BEDF是菱形，

∴S菱形BEDF=BD·EF

=×4×3

=6.