练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】（8分）在学习概率的课堂上，老师提出问题：只有一张电影票，小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影，请你设计一个对小明和小刚都公平的方案．

    甲同学的方案：将红桃2、3、4、5四张牌背面向上，小明先抽一张，小刚从剩下的三张牌中抽一张，若两张牌上的数字之和是奇数，则小明看电影，否则小刚看电影．

    （1）甲同学的方案公平吗？请用列表或画树状图的方法说明；

    （2）乙同学将甲的方案修改为只用红桃2、3、4三张牌，抽取方式及规则不变，乙的方案公平吗？（只回答，不说明理由）

    【答案】（1）公平；（2）不公平．

    【解析】试题分析：(1)、依据题意先用列表法或画树状图法分析所有等可能的出现结果，然后根据概率公式求出该事件的概率，比较即可．(2)、解题思路同上．

    试题解析：(1)、甲同学的方案不公平．理由如下：

    列表法，

    小明
    小刚

    2

    3

    4

    5

    2


    （2，3）

    （2，4）

    （2，5）

    3

    （3，2）


    （3，4）

    （3，5）

    4

    （4，2）

    （4，3）


    （4，5）

    5

    （5，2）

    （5，3）

    （5，4）


    所有可能出现的结果共有12种，其中抽出的牌面上的数字之和为奇数的有：8种，故小明获胜的概率为：=，则小刚获胜的概率为：， 故此游戏两人获胜的概率不相同，即他们的游戏规则不公平；

    (2)、不公平．理由如下：

    小明
    小刚

    2

    3

    4

    2


    （2，3）

    （2，4）

    3

    （3，2）


    （3，4）

    4

    （4，2）

    （4，3）


    所有可能出现的结果共有6种，其中抽出的牌面上的数字之和为奇数的有：4种，故小明获胜的概率为：=，则小刚获胜的概率为：， 故此游戏两人获胜的概率不相同，即他们的游戏规则不公平．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在矩形ABCD中，BE平分∠ABC交CD边于点E．点F在BC边上，且FE⊥AE．如图．

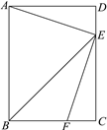
    （1）∠BEC= °；

    （2）在图中已有的三角形中，找到一对全等的三角形，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】每年的6月5日为世界环保日，为提倡低碳环保，某公司决定购买10台节省能源的新机器，现有甲、乙两种型号的机器可选，其中每台的价格、产量如下表：

    甲型机器

    乙型机器

    价格（万元/台）

    a

    b

    产量（吨/月）

    240

    180

    经调查：购买一台甲型机器比购买一台乙型机器多12万元，购买2台甲型机器比购买3台乙型机器多6万元．

    （1） 求a、b的值；

    （2） 若该公司购买新机器的资金不超过216万元，请问该公司有哪几种购买方案？

    （3） 在（2）的条件下，若公司要求每月的产量不低于1890吨，请你为该公司设计一 种最省钱的购买方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某天小明骑自行车上学，途中因自行车发生故障，修车耽误了一段时间后继续骑行，按时赶到了学校．图中描述了他上学的途中离家距离（米）与离家时间（分钟）之间的函数关系．下列说法中正确的个数是（　　）

    （1）修车时间为15分钟；

    （2）学校离家的距离为4000米；

    （3）到达学校时共用时间为20分钟；

    （4）自行车发生故障时离家距离为2000米．

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个不透明的口袋中装有2个红球（记为红1、红2），1个白球、1个黑球，这些球除颜色外都相同，将球搅匀．

    （1）从中任意摸出1个球，恰好摸到红球的概率是 ；

    （2）先从中任意摸出一个球，再从余下的3个球中任意摸出1个球，请用画树状图或列表法求两次都摸到红球的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下图是某校艺术节徽标征集活动4件入围作品，其中是中心对称图形但不是轴对称图形的是（ ）

    A. B.

    C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，如图，平分交于点，点、分别是、的中点，连接，且.

    (1) 求证:；

    (2)连接，若，，求四边形的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点A，B，C的坐标分别为（a，0），（2，﹣4），（c，0），且a，c满足方程为二元一次方程．

    （1）求A，C的坐标．

    （2）若点D为y轴正半轴上的一个动点．

    ①如图1，∠AOD+∠ADO+∠DAO＝180°，当AD∥BC时，∠ADO与∠ACB的平分线交于点P，求∠P的度数；

    ②如图2，连接BD，交x轴于点E．若S△ADE≤S△BCE成立．设动点D的坐标为（0，d），求d的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知，点、分别是直线、上的两点.将射线绕点顺时针匀速旋转，将射线绕点顺时针匀速旋转，旋转后的射线分别记为、，已知射线、射线旋转的速度之和为6度/秒.

    （1）射线先转动得到射线，然后射线、再同时旋转10秒，此时射线与射线第一次出现平行.求射线、的旋转速度；

    （2）若射线、分别以（1）中速度同时转动秒，在射线与射线重合之前，设射线与射线交于点，过点作于点，设，，如图2所示.

    ①当时，求、、满足的数量关系；

    ②当时，求和满足的数量关系.

    查看答案和解析>>

    同步练习册答案