Question

【题目】在矩形ABCD中，BE平分∠ABC交CD边于点E．点F在BC边上，且FE⊥AE．如图．

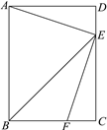
（1）∠BEC= °；

（2）在图中已有的三角形中，找到一对全等的三角形，并证明你的结论．

Answer 1

【答案】（1）45°；（2）（2）△ADE≌△ECF，证明见解析

【解析】

（1）根据矩形的性质得到∠ABC=∠BCD=90°，根据角平分线的定义得到∠EBC=45°，根据三角形内角和定理计算即可；

（2）利用ASA定理证明△ADE≌△ECF．

（1）∵四边形ABCD为矩形，

∴∠ABC=∠BCD=90°，

∵BE平分∠ABC，

∴∠EBC=45°，

∴∠BEC=45°，

故答案为：45；

（2）△ADE≌△ECF，

理由如下：∵四边形ABCD是矩形，

∴∠ABC=∠C=∠D=90°，AD=BC．

∵FE⊥AE，

∴∠AEF=90°．

∴∠AED+∠FEC=180°-∠AEF=90°．

∵∠AED+∠DAE=90°，

∴∠FEC=∠EAD，

∵BE平分∠ABC，

∴∠EBC=∠ABC=45°．

∴∠BEC=45°．

∴∠EBC=∠BEC．

∴BC=EC．

∴AD=EC．

在△ADE和△ECF中，

，

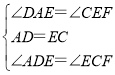∴△ADE≌△ECF．