
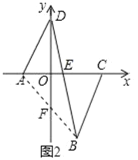
【题目】在平面直角坐标系中,点A,B,C的坐标分别为(a,0),(2,﹣4),(c,0),且a,c满足方程![]() 为二元一次方程.
为二元一次方程.
(1)求A,C的坐标.
(2)若点D为y轴正半轴上的一个动点.
①如图1,∠AOD+∠ADO+∠DAO=180°,当AD∥BC时,∠ADO与∠ACB的平分线交于点P,求∠P的度数;
②如图2,连接BD,交x轴于点E.若S△ADE≤S△BCE成立.设动点D的坐标为(0,d),求d的取值范围.

【答案】(1)A(﹣2,0),C(5,0);(2)①45°;②0<d≤5.
【解析】
(1)根据二元一次方程的定义列式计算;
(2)①作PH∥AD,根据角平分线的定义、平行线的性质计算,得到答案;②连接AB,交y轴于F,根据点的坐标特征分别求出S△ABC、S△ABD,根据题意列出不等式,解不等式即可.
解:(1)由题意得,2a﹣4≠0,c﹣4=1,a2﹣3=1,
解得,a=﹣2,c=5,
则点A的坐标为(﹣2,0),点C的坐标为(5,0);
(2)①作PH∥AD,
∵AD∥BC,
∴PH∥BC,
∵∠AOD=90°,
∴∠ADO+∠OAD=90°,
∵AD∥BC,
∴∠BCA=∠OAD,
∴∠ADO+∠BCA=90°,
∵∠ADO与∠BCA的平分线交于P点,
∴∠ADP=![]() ∠ADO,∠BCP=
∠ADO,∠BCP=![]() ∠BCA,
∠BCA,
∴∠ADP+∠BCP=45°,
∵PH∥AD,PH∥BC,
∴∠HPD=∠ADP,∠HPC=∠BCP,
∴∠DPC=∠HPD+∠HPC=∠ADP+∠BCP=45°;
②连接AB,交y轴于F,
∵S△ADE≤S△BCE,
∴S△ADE+S△ABE≤S△BCE+S△ABE,即S△ABD≤S△ABC,
∵A(﹣2,0),B(2,﹣4),C(5,0),
∴S△ABC=![]() ×(2+5)×4=14,点F的坐标为(0,﹣2),
×(2+5)×4=14,点F的坐标为(0,﹣2),
则S△ABD=![]() ×(2+d)×2+
×(2+d)×2+![]() ×(2+d)×2=4+2d,
×(2+d)×2=4+2d,
由题意得,4+2d≤14,
解得,d≤5,
∵点D为y轴正半轴上的一个动点,
∴0<d≤5.


科目:初中数学 来源: 题型:
【题目】如图,点![]() 在
在![]() 轴上,
轴上, ![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,使点
,使点![]() 与点
与点![]() 重合.
重合.
(1)求点![]() 的坐标;
的坐标;
(2)求经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形?若存在,求出点
为顶点的三角形是等腰三角形?若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌,抽取方式及规则不变,乙的方案公平吗?(只回答,不说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商厦分别用600元购进甲、乙两种糖果,因为甲糖果的进价是乙糖果进价的1.2倍,所以进回的甲糖果的重量比乙糖果少10kg.
(1)甲、乙两种糖果的进价分别是多少?
(2)若两种糖果的销售利润率均为10%,则两种糖果的售价分别是多少?
(3)如果将两种糖果混合在一起销售,总利润不变,那么混合后的糖果单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 与一次函数
与一次函数![]() 的图像交于点
的图像交于点![]() ,
,![]() .
.

(1)求![]() ,
,![]() 的值;
的值;
(2)结合函数图像,写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)![]() 为
为![]() 轴上一点,若
轴上一点,若![]() 的面积是
的面积是![]() 面积的3倍,请求出点
面积的3倍,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,如果AD=2cm,DB=1cm,AE=1.8cm,则EC=( )
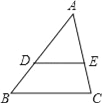
A. 0.9cm B. 1cm C. 3.6cm D. 0.2cm
【答案】A
【解析】试题分析:根据平行线分线段成比例定理得到![]() =
=![]() ,然后利用比例性质求EC的长.
,然后利用比例性质求EC的长.
解:∵DE∥BC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴EC=0.9(cm).
故选A.
考点:平行线分线段成比例.
【题型】单选题
【结束】
6
【题目】点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC等于( )
A. 6 cm B. ![]() cm C.
cm C. ![]() cm D.
cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(3,0),B(0,3),过点B画y轴的垂线l,点C在线段AB上,连结OC并延长交直线l于点D,过点C画CE⊥OC交直线l于点E.
(1)求∠OBA的度数,并直接写出直线AB的解析式;
(2)若点C的横坐标为2,求BE的长;
(3)当BE=1时,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图象上有一点D(x,y)(其中x>0,y>0),使S△ABD=S△ABC,求点D的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com