
【题目】某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.图中描述了他上学的途中离家距离![]() (米)与离家时间
(米)与离家时间![]() (分钟)之间的函数关系.下列说法中正确的个数是( )
(分钟)之间的函数关系.下列说法中正确的个数是( )
(1)修车时间为15分钟;
(2)学校离家的距离为4000米;
(3)到达学校时共用时间为20分钟;
(4)自行车发生故障时离家距离为2000米.

A.1个B.2个C.3个D.4个
【答案】C
【解析】
(1)根据图象中平行于x轴的那一段的时间即可得出答案;
(2)根据图象的纵轴的最大值即可得出答案;
(3)根据图象的横轴的最大值即可得出答案;
(4)根据图象中10分钟时对应的纵坐标即可判断此时的离家距离.
(1)根据图象可知平行于x轴的那一段的时间为15-10=5(分钟),所以修车时间为5分钟,故错误;
(2)根据图象的纵轴的最大值可知学校离家的距离为4000米,故正确;
(3)根据图象的横轴的最大值可知到达学校时共用时间为20分钟,故正确;
(4)根据图象中10分钟时对应的纵坐标为2000,所以自行车发生故障时离家距离为2000米,故正确;
所以正确的有3个.
故选:C.


科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在
在![]() 轴上,
轴上, ![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,使点
,使点![]() 与点
与点![]() 重合.
重合.
(1)求点![]() 的坐标;
的坐标;
(2)求经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形?若存在,求出点
为顶点的三角形是等腰三角形?若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
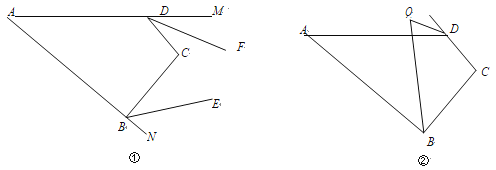
【题目】如图①,在四边形 ABCD 中,∠A=x°,∠C=y°.
(1) ∠ABC+∠ADC= °.(用含 x,y 的代数式表示)
(2) BE、DF 分别为∠ABC、∠ADC 的外角平分线,
①若 BE∥DF,x=30,则 y= ;
②当 y=2x 时,若 BE 与 DF 交于点 P,且∠DPB=20°,求 y 的值.
(3) 如图②,∠ABC 的平分线与∠ADC 的外角平分线交于点 Q,则∠Q= °.(用含 x,y 的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择.其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调査,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂期买机器的预算资金不超过34万元,那么你认为该工厂有哪几种购买方案?
(3)在(2)的条件下,如果要求该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金.应该选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
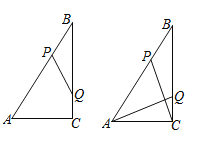
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)当t为何值时,四边形ACQP的面积最小,最小值是多少?
(3)连接AQ,CP,若AQ⊥CP,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌,抽取方式及规则不变,乙的方案公平吗?(只回答,不说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商厦分别用600元购进甲、乙两种糖果,因为甲糖果的进价是乙糖果进价的1.2倍,所以进回的甲糖果的重量比乙糖果少10kg.
(1)甲、乙两种糖果的进价分别是多少?
(2)若两种糖果的销售利润率均为10%,则两种糖果的售价分别是多少?
(3)如果将两种糖果混合在一起销售,总利润不变,那么混合后的糖果单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(3,0),B(0,3),过点B画y轴的垂线l,点C在线段AB上,连结OC并延长交直线l于点D,过点C画CE⊥OC交直线l于点E.
(1)求∠OBA的度数,并直接写出直线AB的解析式;
(2)若点C的横坐标为2,求BE的长;
(3)当BE=1时,求点C的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com