
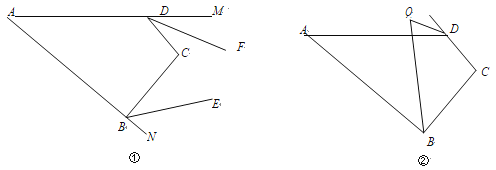
【题目】如图①,在四边形 ABCD 中,∠A=x°,∠C=y°.
(1) ∠ABC+∠ADC= °.(用含 x,y 的代数式表示)
(2) BE、DF 分别为∠ABC、∠ADC 的外角平分线,
①若 BE∥DF,x=30,则 y= ;
②当 y=2x 时,若 BE 与 DF 交于点 P,且∠DPB=20°,求 y 的值.
(3) 如图②,∠ABC 的平分线与∠ADC 的外角平分线交于点 Q,则∠Q= °.(用含 x,y 的代数式表示)
【答案】(1)(360-x-y). (2)①30°;x=40,y=80;(3)90+![]() (x-y)
(x-y)
【解析】
(1)利用四边形内角和是360°即可解题,(2)①作出图像,利用四边形的内角和是360°即可解题, ②利用内角和定理和角平分线的性质得到∠PBC+∠PDC=![]() (∠NBC+∠MDC)=
(∠NBC+∠MDC)=![]() (x+y),再延长 BC,与 DP 交于点 Q,利用三角形的外角的性质即可求解,(3)利用四边形BCDQ和四边形ABCD的内角和是360°,分别表示出两个等式,进行化简整理可得∠A+∠ADC+∠C+2∠1=360°,再利用∠1-∠2=90°-(
(x+y),再延长 BC,与 DP 交于点 Q,利用三角形的外角的性质即可求解,(3)利用四边形BCDQ和四边形ABCD的内角和是360°,分别表示出两个等式,进行化简整理可得∠A+∠ADC+∠C+2∠1=360°,再利用∠1-∠2=90°-(![]() )°,即可求解.
)°,即可求解.
解:(1)∵四边形ABCD的内角和是360°,
∴∠ABC+∠ADC=360°-(∠A+∠B)=(360-x-y)°.
(2)①过点C作CH∥DF,
∵ BE∥DF
∴CH∥BE,∠FDC=∠DCH,∠EBC=∠BCH,
∴∠ABC=180°-2∠CBE,∠ADC=180°-2∠FDC,∠BCD=∠EBC+∠FDC,
∴30°+180°-2∠CBE+∠EBC+∠FDC+180°-2∠FDC=360°,
∴∠EBC+∠FDC=30°,即y=30°,

②由(1)得∠ABC+∠ADC =(360-x-y) °
又∵∠ADC+∠MDC=180°,∠ABC+∠NDC=180°
∴∠NBC+∠MDC=(x+y)°
∵BE、DF 分别为平分∠ABC、∠ADC
∴∠PBC=![]() ∠NBC,∠PDC=
∠NBC,∠PDC=![]() ∠MDC
∠MDC
∴∠PBC+∠PDC=![]() (∠NBC+∠MDC)=
(∠NBC+∠MDC)=![]() (x+y)
(x+y)
延长 BC,与 DP 交于点 Q,见下图,
∵∠BCD=∠PDC+∠DQC,∠DQC=∠P+∠QBP(外角性质)
∴∠BCD=∠P+∠PBC+∠PDC
∴y=20+![]() (x+y),即y-x=40
(x+y),即y-x=40
又∵y=2x
∴x=40,y=80
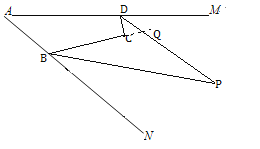
(3)如下图,∵∠ABC 的平分线与∠ADC 的外角平分线交于点 Q,
∴∠ABQ=∠CBQ=∠1,
∵四边形BCDQ和四边形ABCD的内角和是360°,
即∠Q+∠2+∠ADC+∠C+∠1=360°,
∠A+∠ADC+∠C+2∠1=360°,
整理得,∠Q=∠A+(∠1-∠2)
∵∠A+∠ADC+∠C+2∠1=360°,
整理得,∠1-∠2=90°-(![]() )°,
)°,
∴∠Q=[90+![]() (x-y)]°
(x-y)]°



 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形![]() 的底边
的底边![]() 长为
长为![]() ,面积是
,面积是![]() , 腰
, 腰![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 边于
边于![]() 点.若点
点.若点![]() 为
为![]() 边的中点,点
边的中点,点![]() 为线段EF上一动点,则
为线段EF上一动点,则![]() 周长的最小值为( )
周长的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)观察图象,直接写出反比例函数值大于一次函数值x取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为提倡低碳环保,某公司决定购买10台节省能源的新机器,现有甲、乙两种型号的机器可选,其中每台的价格、产量如下表:
甲型机器 | 乙型机器 | |
价格(万元/台) | a | b |
产量(吨/月) | 240 | 180 |
经调查:购买一台甲型机器比购买一台乙型机器多12万元,购买2台甲型机器比购买3台乙型机器多6万元.
(1) 求a、b的值;
(2) 若该公司购买新机器的资金不超过216万元,请问该公司有哪几种购买方案?
(3) 在(2)的条件下,若公司要求每月的产量不低于1890吨,请你为该公司设计一 种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
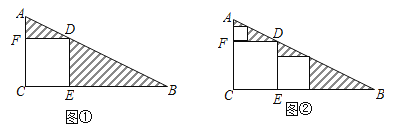
【题目】三角形纸片ABC中,∠C=90°,AC=1,BC=2.按图①的方式在这张纸片中剪去一个尽可能大的正方形,称为第1次剪取,记余下的两个三角形面积和为S1;按图②的方式在余下的Rt△ADF和Rt△BDE中,分别剪去尽可能大的正方形,称为第2次剪取,记余下的两个三角形面积和为S2;继续操作下去…….
(1)如图①,求![]() 和S1的值;
和S1的值;
(2)第n次剪取后,余下的所有三角形面积之和Sn为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.图中描述了他上学的途中离家距离![]() (米)与离家时间
(米)与离家时间![]() (分钟)之间的函数关系.下列说法中正确的个数是( )
(分钟)之间的函数关系.下列说法中正确的个数是( )
(1)修车时间为15分钟;
(2)学校离家的距离为4000米;
(3)到达学校时共用时间为20分钟;
(4)自行车发生故障时离家距离为2000米.

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com