
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

【答案】(1)12(2)当x=11时,y最小=88平方米
【解析】(1)根据题意得方程解即可;
(2)设苗圃园的面积为y,根据题意得到二次函数的解析式y=x(30-2x)=-2x2+30x,根据二次函数的性质求解即可.
解: (1)苗圃园与墙平行的一边长为(30-2x)米.依题意可列方程
x(30-2x)=72,即x2-15x+36=0.
解得x1=3(舍去),x2=12.
(2)依题意,得8≤30-2x≤18.解得6≤x≤11.
面积S=x(30-2x)=-2(x-![]() )2+
)2+![]() (6≤x≤11).
(6≤x≤11).
①当x=![]() 时,S有最大值,S最大=
时,S有最大值,S最大=![]() ;
;
②当x=11时,S有最小值,S最小=11×(30-22)=88
“点睛”此题考查了二次函数、一元二次不等式的实际应用问题,解题的关键是根据题意构建二次函数模型,然后根据二次函数的性质求解即可.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式![]() 进行因式分解的过程.
进行因式分解的过程.
解:设![]() ,
,
原式![]() (第一步)
(第一步)
![]() (第二步)
(第二步)
![]() (第三步)
(第三步)
![]() .(第四步)
.(第四步)
请你回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______;
A.提公因式法 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果不彻底,请直接写出因式分解的最后结果_______;
(3)仿照以上方法因式分解:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
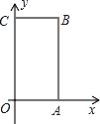
【题目】如图所示,在长方体![]() 中,
中,![]() 为平面直角坐标系的原点,
为平面直角坐标系的原点,![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,点
,点![]() 在第一象限.
在第一象限.
(1) 写出![]() 点坐标;
点坐标;
(2) 若过点![]() 的直线
的直线![]() ,且把
,且把![]() 分为
分为![]() :
:![]() 两部分,求出点
两部分,求出点![]() 的坐标;
的坐标;
(3) 在(2)的条件下,求出四边形![]() 的面积;
的面积;
(4) 若点![]() 是射线
是射线![]() 上的点,请直接写出
上的点,请直接写出![]() ,
,![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3),点D与点C关于抛物线的对称轴对称.
与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3),点D与点C关于抛物线的对称轴对称.

(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线对称轴上的一动点,当△PAC的周长最小时,求出点P的坐标;
(3)若点Q在x轴正半轴上,且∠ADQ=∠DAC,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的方格中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上;
(1)建立适当的平面直角坐标系,使A(﹣2,﹣1),C(1,﹣1),写出B点坐标;
(2)在(1)的条件下,将△ABC向右平移4个单位再向上平移2个单位,在图中画出平移后的△A′B′C′,并分别写出A′、B′、C′的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]()
![]() 中任一点
中任一点![]() 经过平移后对应点为
经过平移后对应点为![]() .将
.将![]()
![]() 作同样的平移得到
作同样的平移得到![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,
,
(1) 在图中画出![]() ,;
,;
(2) 直接写出![]() 的坐标分别为
的坐标分别为![]()
(3) ![]() ,的面积为____________.
,的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.其中正确结论的序号是( )

A. ②④ B. ①③ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A、B两种型号的客车共20辆,它们的载客量、每天的租金如表所示.已知在20辆客车都坐满的情况下,共载客720人.
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
(1)求A、B两种型号的客车各有多少辆?
(2)某中学计划租用A、B两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有305人,请写出所有可能的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com