
【题目】如图![]()
![]() 中任一点
中任一点![]() 经过平移后对应点为
经过平移后对应点为![]() .将
.将![]()
![]() 作同样的平移得到
作同样的平移得到![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,
,
(1) 在图中画出![]() ,;
,;
(2) 直接写出![]() 的坐标分别为
的坐标分别为![]()
(3) ![]() ,的面积为____________.
,的面积为____________.
【答案】(1)见解析;(2)A1(5,1),B1(1,-1),C1(3,-4);(3)8.
【解析】
(1)先根据点P(m,n)经平移后对应点为P1(m+4,n-3),得到平移的方向与距离,再进行画图;
(2)根据平移的方向与距离,写出A1,B1,C1的坐标;
(3)根据割补法可以求△A1B1C1的面积.
解:(1)∵点P(m,n)经平移后对应点为P1(m+4,n-3),
∴△ABC向右平移4个单位,向下平移3个单位可以得到△A1B1C1,如图所示:
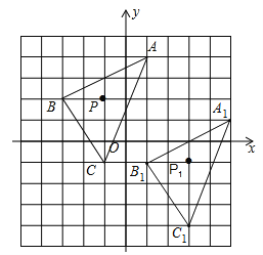
△A1B1C1即为所求;
(2)∵A(1,4),B(-3,2),C(-1,-1),
∴A1,B1,C1的坐标分别为A1(5,1),B1(1,-1),C1(3,-4);
(3)△A1B1C1的面积为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得⊿CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由.
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知射线CB∥OA,∠C=∠OAB,
(1)求证:AB∥OC;
(2)如图2,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
①当∠C=110°时,求∠EOB的度数.
②若平行移动AB,那么∠OBC :∠OFC的值是否随之发生变化?若变化,找出变
化规律;若不变,求出这个比值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知A(a,0),B(b,3),C(4,0),且满足(a+b)2+|a﹣b+6|=0,线段AB交y轴于F点.
(1)求点A、B的坐标;
(2)点D为y轴正半轴上一点,若ED∥AB,且AM,DM分别平分∠CAB,∠ODE,如图 2,求∠AMD的度数;
(3)如图 3,(也可以利用图 1)①求点F的坐标;②坐标轴上是否存在点P,使得△ABP和△ABC的面积相等?若存在,求出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小华根据学习函数的经验,对函数
的图象与性质.小华根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)在函数![]() 中,自变量x的取值范围是________.
中,自变量x的取值范围是________.
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 5 | 4 | 3 | 2 | 1 | 0 | 1 | 2 | m | … |
①求m的值;
②在平面直角坐标系xOy中,描出以上表中各组对应值为坐标的点,并根据描出的点,画出该函数的图象.

(2)结合函数图象写出该函数的一条性质:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校随机抽取部分学生,调查每个月的零花钱消费额,数据整理成如下的统计表和如图①②所示的两幅不完整的统计图,已知图①中A,E两组对应的小长方形的高度之比为2:1请结合相关数据解答以下问题:
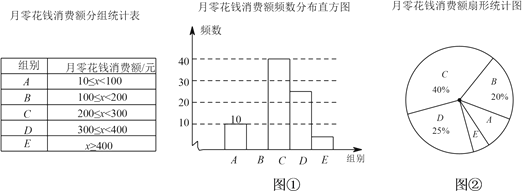
(1)本次调查样本的容量是______;
(2)补全频数分布直方图,并标明各组的频数;
(3)若该学校有2500名学生,请估计月消费零花钱不少于300元的学生的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人骑自行车前往A地,他们距A地的路程s(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:

(1)甲、乙两人的速度各是多少?
(2)求出甲距![]() 地的路程
地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数关系式.
之间的函数关系式.
(3)在什么时间段内乙比甲离![]() 地更近?
地更近?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com