Question

【题目】抛物线与x轴交于A，B两点（A在B的左侧），与y轴交于点C（0，－3），点D与点C关于抛物线的对称轴对称．

（1）求抛物线的解析式及点D的坐标；

（2）点P是抛物线对称轴上的一动点，当△PAC的周长最小时，求出点P的坐标；

（3）若点Q在x轴正半轴上，且∠ADQ＝∠DAC，求出点Q的坐标．

Answer 1

【答案】（1）抛物线的解析式为，点D的坐标为（2，－3）；

（2）点P的坐标为（1，－2）；

（3）Q点坐标为（1，0）.

【解析】试题分析：（1）利用待定系数法即可求出n，利用对称性C、D关于对称轴对称即可求出点D坐标．

（2）A，P，D三点在同一直线上时△PAC的周长最小，求出直线AD的解析式即可解决问题．

（3）分两种情形①作DQ∥AC交x轴于点Q，此时∠DQA=∠DAC，满足条件．②设线段AD的垂直平分线交AC于E，直线DE与x的交点为Q′，此时∠Q′DA=′CAD，满足条件，分别求解即可．

试题解析：（1）把C(0，3)代入y=(x1)2+n，得3=(01)2+n，

解得n=4，

∴抛物线的解析式为y=(x1)24，

∴抛物线的对称轴为直线x=1，

∵点D与点C关于抛物线的对称轴对称，

∴点D的坐标为(2，3).

（2）连接PA、PC、PD，

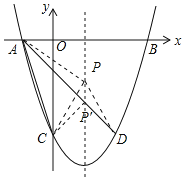
∵点D与点C关于抛物线的对称轴对称，

∴PC=PD，

∴AC+PA+PC=AC+PA+PD，

∵AC为定值，PA+PDAD，

∴当PA+PC的值最小，即A，P，D三点在同一直线上时△PAC的周长最小，

由y=(x1)24=0解得：x1=1，x2=3，

∵A在B的左侧，

∴A(1，0)，

由A，D两点坐标可求得直线AD的解析式为y=x1，

当x=1时，y=x1=2，

∴当△PAC的周长最小时，点P的坐标为(1，2)；

（3）如图中，作DQ∥AC交x轴于点Q，此时∠DQA=∠DAC，满足条件，

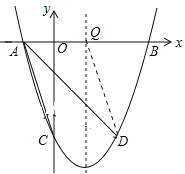
∵A(1，0)，C(0，3)，

∴直线AC的解析式为y=3x3，

∴直线QD的解析式为y=3x+3，

令y=0，得x=1，

∴Q(1，0).