
【题目】在图1,2,3中,已知![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上的动点,连接
上的动点,连接![]() ,以
,以![]() 为边向上作菱形
为边向上作菱形![]() ,且
,且![]() .
.
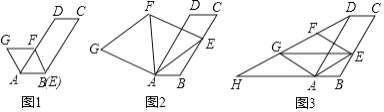
(1)如图1,当点![]() 与点
与点![]() 重合时,
重合时,![]() ________°;
________°;
(2)如图2,连接![]() .
.
①填空:![]() _________
_________![]() (填“>”,“<”,“=”);
(填“>”,“<”,“=”);
②求证:点![]() 在
在![]() 的平分线上;
的平分线上;
(3)如图3,连接![]() ,
,![]() ,并延长
,并延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,当四边形
,当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的值.
的值.
【答案】(1)60°;(2)① =,②见解析;(3)3
【解析】
(1)根据菱形的性质计算;
(2)①证明![]() ,根据角的运算解答;
,根据角的运算解答;
②作![]() 于
于![]() ,
,![]() 交
交![]() 的延长线于
的延长线于![]() ,证明
,证明![]() ,根据全等三角形的性质得到
,根据全等三角形的性质得到![]() ,根据角平分线的判定定理证明结论;
,根据角平分线的判定定理证明结论;
(3)根据直角三角形的性质得到![]() ,证明四边形
,证明四边形![]() 为菱形,根据菱形的性质计算,得到答案.
为菱形,根据菱形的性质计算,得到答案.
解:(1)![]() 四边形
四边形![]() 是菱形,
是菱形,
![]() ,
,
![]() ,
,
故答案为![]() ;
;
(2)①![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() 四边形
四边形![]() 是菱形,
是菱形,![]() ,
,
![]() ,
,
![]() ,
,
故答案为![]() ;
;
②作![]() 于
于![]() ,
,![]() 交
交![]() 的延长线于
的延长线于![]() ,
,
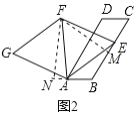
则![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
在![]() 和
和![]() 中,
中,
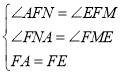 ,
,
![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,
![]() 点
点![]() 在
在![]() 的平分线上;
的平分线上;
(3)![]() 四边形
四边形![]() 是菱形,
是菱形,![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
![]() 平行四边形
平行四边形![]() 为菱形,
为菱形,
![]() ,
,
![]() ,
,
![]()
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
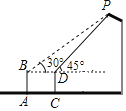
【题目】小明同学在数学实践活动课中测景路灯的高度,如图,已知她的目高AB为1.5米,街为站在A处看路灯顶端P的仰角为30°.再往前走2米站在C处,看路灯顶端P的仰角为45°,求路灯顶端P到地面的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是 .(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:
①m= ,n= ;
②补全条形统计图;
③扇形统计图中扇形C的圆心角度数是 ;
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
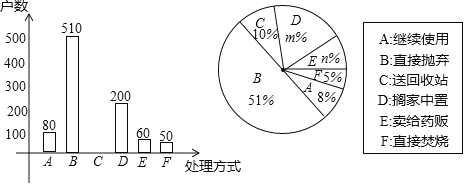
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:

(1)求本次比赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABMN中,AN=1,点C是MN的中点,分別连接AC,BC,且BC=2,点D为AC的中点,点E为边AB上一个动点,连接DE,点A关于直线DE的对称点为点F,分别连接DF,EF.当EF⊥AC时,AE的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年某企业按餐厨垃圾处理费25元/吨,建筑垃圾处理费16元/吨标准,共支付餐厨和建筑垃圾处理费5200元,从2014年元月起,收费标准上调为:餐厨垃圾处理费100元/吨,建筑垃圾处理费30元/吨,若该企业2014年处理的这两种垃圾数量与2013年相比没有变化,就要多支付垃圾处理费8800元,
(1)该企业2013年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2014年将上述两种垃圾处理量减少到240吨,且建筑垃圾处理费不超过餐厨垃圾处理量的3倍,则2014年该企业最少需要支付这两种垃圾处理费共多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com