
【题目】如图,在矩形ABMN中,AN=1,点C是MN的中点,分別连接AC,BC,且BC=2,点D为AC的中点,点E为边AB上一个动点,连接DE,点A关于直线DE的对称点为点F,分别连接DF,EF.当EF⊥AC时,AE的长为________.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图1,点![]() 是数轴上:从左到右排列的三个点,分别对应的数为
是数轴上:从左到右排列的三个点,分别对应的数为![]() 某同学将刻度尺如图2放置.使刻度尺上的数字
某同学将刻度尺如图2放置.使刻度尺上的数字![]() 对齐数轴上的点
对齐数轴上的点![]() ,发现点
,发现点![]() 对齐刻度
对齐刻度![]() ,点
,点![]() 对齐刻度
对齐刻度![]() .
.
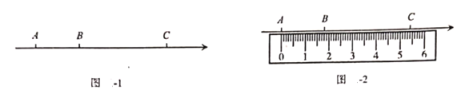
(1)在图1的数轴上,![]() 个单位长度;数轴上的一个单位长度对应刻度尺上的
个单位长度;数轴上的一个单位长度对应刻度尺上的 ![]() .
.
(2)求数轴上点![]() 所对应的数
所对应的数![]() ;
;
(3)在图1的数轴上,点![]() 是线段
是线段![]() 上一点,满足
上一点,满足![]() 求点
求点![]() 所表示的数.
所表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图1,2,3中,已知![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上的动点,连接
上的动点,连接![]() ,以
,以![]() 为边向上作菱形
为边向上作菱形![]() ,且
,且![]() .
.
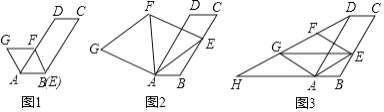
(1)如图1,当点![]() 与点
与点![]() 重合时,
重合时,![]() ________°;
________°;
(2)如图2,连接![]() .
.
①填空:![]() _________
_________![]() (填“>”,“<”,“=”);
(填“>”,“<”,“=”);
②求证:点![]() 在
在![]() 的平分线上;
的平分线上;
(3)如图3,连接![]() ,
,![]() ,并延长
,并延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,当四边形
,当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=45°,点D为射线BC上一动点(与点B、C不重合),连接AD,以AD为一边在AD一侧作正方形ADEF(如图1).
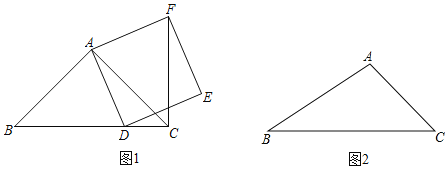
(1)如果AB=AC,且点D在线段BC上运动,证明:CF⊥BD;
(2)如果AB≠AC,且点D在线段BC的延长线上运动,请在图2中画出相应的示意图,此时(1)中的结论是否成立?请说明理由;
(3)设正方形ADEF的边DE所在直线与直线CF相交于点P,若AC=4,CD=2,求线段CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是平面内不与点
是平面内不与点![]() 重合的任意一点,连接
重合的任意一点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点.
的中点.
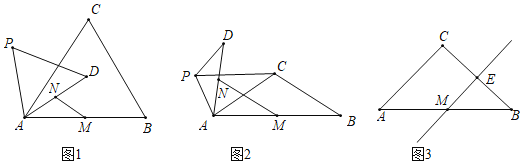
(1)问题发现:
如图1,当![]() 时,
时,![]() 的值是_________,直线
的值是_________,直线![]() 与直线
与直线![]() 相交所成的较小角的度数是________.
相交所成的较小角的度数是________.
(2)类比探究:
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 相交所成的较小角的度数,并说明理由.
相交所成的较小角的度数,并说明理由.
(3)解决问题:
如图3,当![]() 时,若
时,若![]() 是
是![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,且点
上,且点![]() 在同一条直线上,请直接写出
在同一条直线上,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)画出△ABC关于x对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我国许多地方严重的“旱情”,为了鼓励居民节约用水,区政府计划实行两级收费制,即每月用水量不超过14吨(含14吨)时,每吨按政府补贴优惠价收费;每月超过14吨时,超过部分每吨按市场调节价收费.小英家1月份用水20吨,交水费29元;2月份用水18吨,交水费24元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点E(x0,yo),点F(x2.y2),点M(x1,y1)是线段EF的中点,则x1=![]() ,y1=
,y1=![]() .在平面直角坐标系中有三个点A(1,﹣1),B(﹣1,﹣1),C(0,1),点P(0,2)关于点A的对称点P1(即P,A,P1三点共线,且PA=P1A),P1关于点B的对称点P2,P2关于点C的对称点P3,…按此规律继续以A,B,C三点为对称点重复前面的操作.依次得到点P4,P5,P6…,则点P2020的坐标是( )
.在平面直角坐标系中有三个点A(1,﹣1),B(﹣1,﹣1),C(0,1),点P(0,2)关于点A的对称点P1(即P,A,P1三点共线,且PA=P1A),P1关于点B的对称点P2,P2关于点C的对称点P3,…按此规律继续以A,B,C三点为对称点重复前面的操作.依次得到点P4,P5,P6…,则点P2020的坐标是( )
A.(4,0)B.(﹣2,2)C.(2,﹣4)D.(﹣4,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com