
【题目】在![]() 中,
中,![]() ,
,![]() 是平面内不与点
是平面内不与点![]() 重合的任意一点,连接
重合的任意一点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点.
的中点.
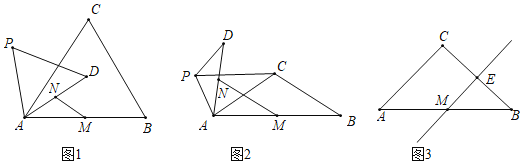
(1)问题发现:
如图1,当![]() 时,
时,![]() 的值是_________,直线
的值是_________,直线![]() 与直线
与直线![]() 相交所成的较小角的度数是________.
相交所成的较小角的度数是________.
(2)类比探究:
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 相交所成的较小角的度数,并说明理由.
相交所成的较小角的度数,并说明理由.
(3)解决问题:
如图3,当![]() 时,若
时,若![]() 是
是![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,且点
上,且点![]() 在同一条直线上,请直接写出
在同一条直线上,请直接写出![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ,见解析;(3)
,见解析;(3)![]() 的值是
的值是![]() 或
或![]()
【解析】
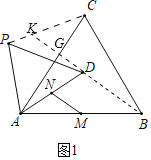
(1)如图1中,连接PC,BD,延长BD交PC于K,交AC于G.证明△PAC≌△DAB(SAS),利用全等三角形的性质以及三角形的中位线定理即可解决问题.
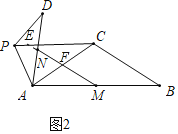
(2)如图2,设MN交AC于F,延长MN交PC于E.证明△ACP∽△AMN,推出∠ACP=∠AMN,![]() 可得结论;
可得结论;
(3)分两种情形分别画出图形,利用三角形中位线定理即可解决问题.
解:(1)![]() ,
,![]()
如图1,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,
![]() ,
,
![]() 均是等边三角形,
均是等边三角形,
![]() ,
,
![]() ,
,
在△PAC和△DAB中,
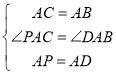 ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中位线,
的中位线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 与
与![]() 相交所成的较小角的度数是
相交所成的较小角的度数是![]() ,
,
![]() ,
,
![]() 与
与![]() 相交所成的较小角的度数是
相交所成的较小角的度数是![]() ;
;
(2)![]() ,直线
,直线![]() 与直线
与直线![]() 相交所成的较小角的度数是
相交所成的较小角的度数是![]() ,
,
理由:如图2,设![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即直线![]() 与直线
与直线![]() 相交所成的较小角的度数是
相交所成的较小角的度数是![]() ;
;
(3)![]() 或
或![]()
设![]() ,由(2)易知,
,由(2)易知,![]() ,
,
![]() ,
,
![]() 是
是![]() 的中位线,
的中位线,![]() ,
,
![]() 是线段
是线段![]() 的中垂线,
的中垂线,
![]() ,
,
![]() 是
是![]() 的中位线,
的中位线,
![]() ,
,
如图3-1,当点![]() 在线段
在线段![]() 上时,
上时,![]() ,
,
![]() ,
,
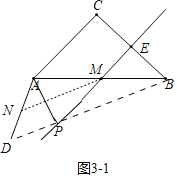
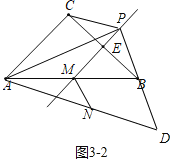
如3-2图,当点![]() 在直线
在直线![]() 上但不在线段
上但不在线段![]() 上时,
上时,![]()
![]() ;
;
综上,![]() 的值是
的值是![]() 或
或![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 铀交于
铀交于![]() 两点(点
两点(点![]() 作点
作点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() 且
且![]() ,点
,点![]() 为抛物线
为抛物线![]() 的对称轴右侧图象上的一点.
的对称轴右侧图象上的一点.
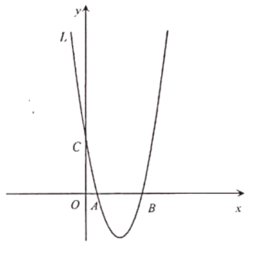
(1)a的值为_ ,抛物线的顶点坐标为_ ;
(2)设抛物线![]() 在点
在点![]() 和点
和点![]() 之间部分(含点
之间部分(含点![]() 和点
和点![]() )的最高点与最低点的纵坐标之差为
)的最高点与最低点的纵坐标之差为![]() ,求
,求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当点![]() 的坐标满足:
的坐标满足:![]() 时,连接
时,连接![]() ,若
,若![]() 为线段
为线段![]() 上一点,且
上一点,且![]() 分四边形
分四边形![]() 的面积为相等两部分,求点
的面积为相等两部分,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意;B级:满意;C级:基本满意;D级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
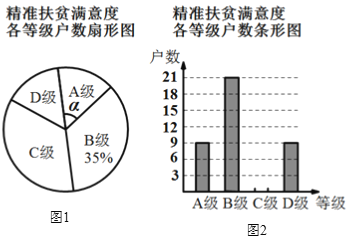
(1)本次抽样调查测试的建档立卡贫困户的总户数______.
(2)图1中,∠α的度数是______,并把图2条形统计图补充完整.
(3)某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的人数约为多少户?
(4)调查人员想从5户建档立卡贫困户(分别记为![]() )中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户
)中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABMN中,AN=1,点C是MN的中点,分別连接AC,BC,且BC=2,点D为AC的中点,点E为边AB上一个动点,连接DE,点A关于直线DE的对称点为点F,分别连接DF,EF.当EF⊥AC时,AE的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
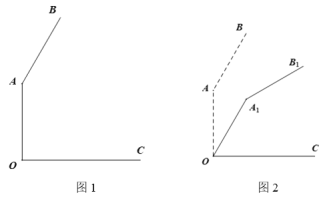
【题目】图1是某品牌台灯竖直摆放在水平桌面上的侧面示意图,其中![]() 为桌面(台灯底座的厚度忽略不计),台灯支架
为桌面(台灯底座的厚度忽略不计),台灯支架![]() 与灯管
与灯管![]() 的长度都为
的长度都为![]() ,且夹角为
,且夹角为![]() (即
(即![]() ),若保持该夹角不变,当支架
),若保持该夹角不变,当支架![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 时,支架与灯管落在
时,支架与灯管落在![]() 位置(如图2所示),则灯管末梢
位置(如图2所示),则灯管末梢![]() 的高度会降低_______
的高度会降低_______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
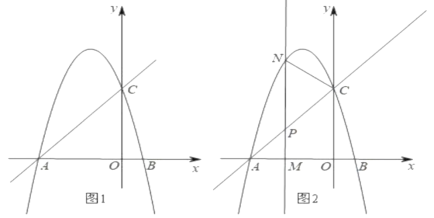
【题目】如图1,直线y=x+c与x轴交于点A(-3,0),与y轴交于点C,抛物线y=-x2+bx+c经过点A、C.
(1)求抛物线的解析式;
(2)如图2所示,M是线段0A上一个动点,过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N.若以C、P、N为顶点的三角形与△APM相似,求四边形MNCO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别与边AB,BC所在的直线相交,交点分别为E,F.
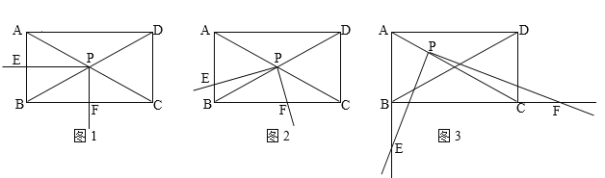
(1)当PE⊥AB,PF⊥BC时,如图1,则![]() 的值为 ;
的值为 ;
(2)在(1)的基础上,现将三角板绕点P逆时针旋转![]() (0°<
(0°<![]() <60°)角,如图2,求
<60°)角,如图2,求![]() 的值;
的值;
(3)若与(2)相比只有如下变化,点P在线段AC上,且AP:PC=1:2,旋转角度![]() ,满足60°<
,满足60°<![]() <90°时,即如图3示,
<90°时,即如图3示,![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】最近,受气温变暖趋势及频繁的大风影响,全球正在进人新一轮的森林火灾高发期,3月30日西昌泸山森林突发火灾,火势迅速向四周蔓延.直接威胁马道街道办事处和西昌城区安全有关部门紧急部署,疏散附近居民.并且组织了一批救灾帐篷和食品以备居民使用.已知帐篷和食品共680件,且帐篷比食品多200件.
(1)求帐篷和食品各多少件.
(2)现计划租用A,B两种货车共16辆,一次性将物资送往灾区,已知A种货车可装帐篷40件和食品10件,B种货车可装帐篷20件和食品20件,请设计一下,共有几种租车方案?
(3)在(2)的条件下,A种货车每辆需运费800元,B种货车每辆需运费720元,怎样租车才能使总运费最少?最少运费是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com