
【题目】最近,受气温变暖趋势及频繁的大风影响,全球正在进人新一轮的森林火灾高发期,3月30日西昌泸山森林突发火灾,火势迅速向四周蔓延.直接威胁马道街道办事处和西昌城区安全有关部门紧急部署,疏散附近居民.并且组织了一批救灾帐篷和食品以备居民使用.已知帐篷和食品共680件,且帐篷比食品多200件.
(1)求帐篷和食品各多少件.
(2)现计划租用A,B两种货车共16辆,一次性将物资送往灾区,已知A种货车可装帐篷40件和食品10件,B种货车可装帐篷20件和食品20件,请设计一下,共有几种租车方案?
(3)在(2)的条件下,A种货车每辆需运费800元,B种货车每辆需运费720元,怎样租车才能使总运费最少?最少运费是多少元?
【答案】(1)帐篷有440件,食品有240件;(2)有3种方案:A种车分别为6,7,8辆,B种车对应为10,9,8辆;(3)当a=6时,即租用A种货车6辆,B种货车10辆,总运费最少,最少运费是12000元
【解析】
(1)首先设帐篷有x件,食品有y件,根据已知条件可以列出方程组,解方程组即可求解;
(2)设租用A种货车a辆,则租用B种货车(16-a)辆,根据已知条件可以列出不等式组,解不等式组即可求解;
(3)设总费用为W元,则根据已知条件列出函数解析式W=800a+720(16-a)=80a+11520,然后利用一次函数的性质和(2)的结论即可求解.
解:(1)设帐篷有x件,食品有y件.
则![]() ,
,
解得![]() ,
,
答:帐篷有440件,食品有240件
(2)设租用A种货车a辆,则租用B种货车(16﹣a)辆,
则![]() ,
,
解得6≤a≤8.
故有3种方案:A种车分别为6,7,8辆,B种车对应为10,9,8辆
(3)设总费用为W元,则
W=800a+720(16﹣a)=80a+11520,
k=80>0,W随a的增大而减少,
所以当a=6时,即租用A种货车6辆,B种货车10辆,总运费最少,最少运费是12000元.


科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是平面内不与点
是平面内不与点![]() 重合的任意一点,连接
重合的任意一点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点.
的中点.
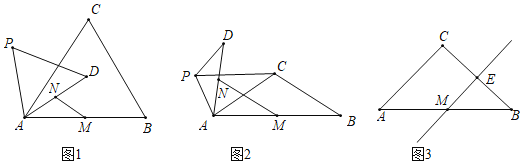
(1)问题发现:
如图1,当![]() 时,
时,![]() 的值是_________,直线
的值是_________,直线![]() 与直线
与直线![]() 相交所成的较小角的度数是________.
相交所成的较小角的度数是________.
(2)类比探究:
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 相交所成的较小角的度数,并说明理由.
相交所成的较小角的度数,并说明理由.
(3)解决问题:
如图3,当![]() 时,若
时,若![]() 是
是![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,且点
上,且点![]() 在同一条直线上,请直接写出
在同一条直线上,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图。请根据图中信息,解答下列问题:
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922393511583744/1923977001213952/STEM/d5900c7cb9b84a9a89aefef7d82bcf93.png]
(1)这次被调查的总人数是多少?
(2)试求表示A组的扇形圆心角的度数,并补全条形统计图;
(3)如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图正比例函数y=k1x与反比例函数y=![]() 的图象相交于A、B两点,AC⊥x轴于点C,CD∥AB交y轴于点D,连接AD、BD,若S△ABD=6,则下列结论正确的是( )
的图象相交于A、B两点,AC⊥x轴于点C,CD∥AB交y轴于点D,连接AD、BD,若S△ABD=6,则下列结论正确的是( )
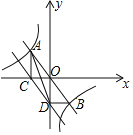
A.k1=﹣6B.k1=﹣3C.k2=﹣6D.k2=﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点E(x0,yo),点F(x2.y2),点M(x1,y1)是线段EF的中点,则x1=![]() ,y1=
,y1=![]() .在平面直角坐标系中有三个点A(1,﹣1),B(﹣1,﹣1),C(0,1),点P(0,2)关于点A的对称点P1(即P,A,P1三点共线,且PA=P1A),P1关于点B的对称点P2,P2关于点C的对称点P3,…按此规律继续以A,B,C三点为对称点重复前面的操作.依次得到点P4,P5,P6…,则点P2020的坐标是( )
.在平面直角坐标系中有三个点A(1,﹣1),B(﹣1,﹣1),C(0,1),点P(0,2)关于点A的对称点P1(即P,A,P1三点共线,且PA=P1A),P1关于点B的对称点P2,P2关于点C的对称点P3,…按此规律继续以A,B,C三点为对称点重复前面的操作.依次得到点P4,P5,P6…,则点P2020的坐标是( )
A.(4,0)B.(﹣2,2)C.(2,﹣4)D.(﹣4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
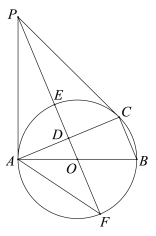
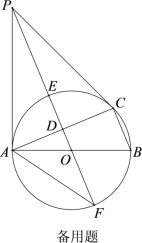
【题目】如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
(1)求证:PA是⊙O的切线;
(2)证明:![]() ;
;
(3)若BC=8,tan∠AFP=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
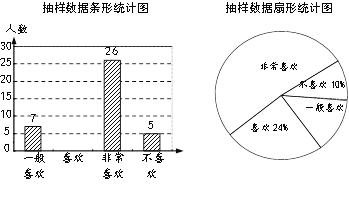
【题目】某校用随机抽样的方法在九年级开展了“你是否喜欢网课”的调查,并将得到的数据整理成了以下统计图(不完整).
(1)此次共调查了 名学生;
(2)请将条形统计图补充完整;
(3)若该学校九年级共有300名学生,请你估计其中“非常喜欢”网课的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com