
����Ŀ����ͼ����֪�����߾�����A����1��0����B��4��0����C��0��2�����㣬��D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M��
��1���������������ʾ�Ķ��κ����ı���ʽ��
��2����֪��F��0��![]() ��������P��x�����˶�ʱ������mΪ��ֵʱ���ı���DMQF��ƽ���ı��Σ�
��������P��x�����˶�ʱ������mΪ��ֵʱ���ı���DMQF��ƽ���ı��Σ�
��3����P���߶�AB�˶������У��Ƿ���ڵ�Q��ʹ���Ե�B��Q��MΪ��������������BOD���ƣ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��y=��![]() x2+
x2+![]() x+2����2��m=��1��m=3ʱ���ı���DMQF��ƽ���ı��Σ���3����Q������Ϊ��3��2����1��0��ʱ���Ե�B��Q��MΪ��������������BOD���ƣ�
x+2����2��m=��1��m=3ʱ���ı���DMQF��ƽ���ı��Σ���3����Q������Ϊ��3��2����1��0��ʱ���Ե�B��Q��MΪ��������������BOD���ƣ�
��������
��1������ϵ�������ɵã�
��2�������ô���ϵ�������ֱ��BD����ʽΪy=![]() x-2����Q��m��-
x-2����Q��m��-![]() m2+
m2+![]() m+2����M��m��
m+2����M��m��![]() m-2������QM��DF���ı���DMQF��ƽ���ı���֪QM=DF���ݴ��г�����m�ķ��̣���֮�ɵã�
m-2������QM��DF���ı���DMQF��ƽ���ı���֪QM=DF���ݴ��г�����m�ķ��̣���֮�ɵã�
��3����֪��ODB=��QMB���ʷ֢١�DOB=��MBQ=90����������DOB�ס�MBQ��![]() ����֤��MBQ�ס�BPQ��
����֤��MBQ�ס�BPQ��![]() ����
����![]() ����֮���ɵô�ʱm��ֵ���ڡ�BQM=90������ʱ��Q���A�غϣ���BOD�ס�BQM�����õ�Q���꣮
����֮���ɵô�ʱm��ֵ���ڡ�BQM=90������ʱ��Q���A�غϣ���BOD�ס�BQM�����õ�Q���꣮
��1���������߹���A��-1��0����B��4��0���������ʽΪy=a��x+1����x-4����
����C��0��2�����룬�ã�-4a=2��
��ã�a=-![]() ��
��
�������߽���ʽΪy=-![]() ��x+1����x-4��=-
��x+1����x-4��=-![]() x2+
x2+![]() x+2��
x+2��
��2��������֪��D����Ϊ��0��-2����
��ֱ��BD����ʽΪy=kx+b��
��B��4��0����D��0��-2�����룬�ã�
![]() ����ã�
����ã�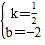 ��
��
��ֱ��BD����ʽΪy=![]() x-2��
x-2��
��QM��x�ᣬP��m��0����
��Q��m��--![]() m2+
m2+![]() m+2����M��m��
m+2����M��m��![]() m-2����
m-2����
��QM=-![]() m2+
m2+![]() m+2-��
m+2-��![]() m-2��=-
m-2��=-![]() m2+m+4��
m2+m+4��
��F��0��![]() ����D��0��-2����
����D��0��-2����
��DF=![]() ��
��
��QM��DF��
�൱-![]() m2+m+4=
m2+m+4=![]() ʱ���ı���DMQF��ƽ���ı��Σ�
ʱ���ı���DMQF��ƽ���ı��Σ�
��ã�m=-1���ᣩ��m=3��
��m=3ʱ���ı���DMQF��ƽ���ı��Σ�
��3����ͼ��ʾ��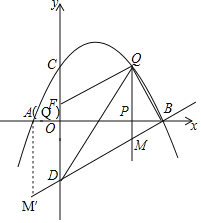
��QM��DF��
���ODB=��QMB��
���������������
�ٵ���DOB=��MBQ=90��ʱ����DOB�ס�MBQ��
��![]() ��
��
�ߡ�MBQ=90�㣬
���MBP+��PBQ=90�㣬
�ߡ�MPB=��BPQ=90�㣬
���MBP+��BMP=90�㣬
���BMP=��PBQ��
���MBQ�ס�BPQ��
��![]() ����
����![]() ��
��
��ã�m1=3��m2=4��
��m=4ʱ����P��Q��M�����B�غϣ����ܹ��������Σ���ȥ��
��m=3����Q��������3��2����
�ڵ���BQM=90��ʱ����ʱ��Q���A�غϣ���BOD�ס�BQM�䣬
��ʱm=-1����Q������Ϊ��-1��0����
���ϣ���Q������Ϊ��3��2����-1��0��ʱ���Ե�B��Q��MΪ���������������BOD���ƣ�


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ף�������ͬʱ��������600������ļӹ����ױ���ÿ���Ӽӹ��������࣬����ͬʱ��ʼ�ӹ����ӹ�����������һ�������ֹͣ�ӹ������Ӻ��ּ�����ԭ�ټӹ���ֱ���������������ͼ��ʾ�ױ��Ҷ�ӹ����������y��������ӹ�ʱ��x���֣�֮��ĺ�����ϵ���۲�ͼ�����������⣺
��1����B��������_____��B���ʾ��ʵ��������_____��
��2�����߶�BC��Ӧ�ĺ�����ϵʽ��D�����ꣻ
��3�����ڼӹ��Ĺ����У����ٷ���ʱ�ȼ��ټӹ�100�������
��4��Ϊ��ʹ�������ͬʱ����������ñ����Ҽӹ���ֱ����ɣ���ÿ�����ܼӹ�3����������ѱ��ӹ�������������ҵ����£��ʱ�Ӧ�ڵڶ��ٷ���ʱ��ʼ�����ң�����ͼ������������������y��x֮��ĺ�����ϵ��ͼ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽������ͼ1������ABC�У���D��BC���е㣬DE��DF��DE��AB�ڵ�E��DF��AC�ڵ�F������EF��

��BE��CF��EF֮��Ĺ�ϵΪ��BE+CF�� EF������������������������������
������A��90����̽���߶�BE��CF��EF֮��ĵ�����ϵ��������֤����
����������ͼ2�����ı���ABDC�У���B+��C��180����DB��DC����BDC��130������DΪ��������EDF��65������EDF�����߷ֱ�AB��AC��E��F���㣬����EF��̽���߶�BE��CF��EF֮���������ϵ��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Rt��ABC�У���ACB��90�㣬ֱ��l����C��
��1����AC��BCʱ����ͼ1���ֱ����A��B��AD��ֱ��l�ڵ�D��BE��ֱ��l�ڵ� E����ACD���CBE�Ƿ�ȫ�ȣ���˵�����ɣ�
��2����AC��9cm��BC��6cmʱ����ͼ2����B���F����ֱ��l�Գƣ�����BF��CF����M��AC�ϣ���N��CF��һ�㣬�ֱ����M��N��MD��ֱ��l�ڵ�D��NE��ֱ��l�ڵ�E����M��A���������ÿ��1cm���ٶ���A��C·���˶����յ�ΪC����N�ӵ�F��������ÿ��3cm���ٶ���F��C��B��C��F·���˶����յ�ΪF����M��Nͬʱ��ʼ�˶������Դﵽ��Ӧ���յ�ʱֹͣ�˶������˶�ʱ��Ϊt�룮
������CMNΪ����ֱ��������ʱ����t��ֵ��
������MDC���CENȫ��ʱ����t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��2015��Ϊ����������ƶ����Ͷ���ʽ�1280��Ԫ������ذ��ã����滮Ͷ���ʽ��������ӣ�2017����2015��Ļ���������Ͷ���ʽ�1600��Ԫ��
��1����2015�굽2017�꣬�õ�Ͷ����ذ����ʽ����ƽ��������Ϊ���٣�
��2����2017����ذ��õľ���ʵʩ�У��õؼƻ�Ͷ���ʽ���500��Ԫ�������Ȱ�Ǩ�ⷿ�������涨ǰ1000��������1000����ÿ��ÿ�콱��8Ԫ��1000���Ժ�ÿ��ÿ�콱��5Ԫ�����ⷿ400����㣬��2017��õ������ж��ٻ����ܵ����Ȱ�Ǩ�ⷿ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���֪��D��E��F�ֱ�ΪBC��AD��AE���е㣬��S��ABC=4cm2������Ӱ�������S=��������cm2��
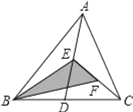
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB=AC�������������ĸ����������ж���ABE�ա�ACD�� ��
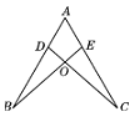
A.��B=��CB.AD=AEC.BD=CED.BE=CD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�ֳɱ�Ϊÿ��60Ԫ�ķ�װ���涨�����ڼ����۵��۲����ڳɱ����ۣ��һ������ø���45%�����������֣�������y�����������۵���x��Ԫ������һ�κ���y=kx+b����x=65ʱ��y=55��x=75ʱ��y=45��
��1����һ�κ���y=kx+b�ı���ʽ��
��2�������̳��������ΪWԪ����д������W�����۵���x֮��Ĺ�ϵʽ�����۵��۶�Ϊ����Ԫʱ���̳��ɻ�����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com