
����Ŀ��Rt��ABC�У���ACB��90�㣬ֱ��l����C��
��1����AC��BCʱ����ͼ1���ֱ����A��B��AD��ֱ��l�ڵ�D��BE��ֱ��l�ڵ� E����ACD���CBE�Ƿ�ȫ�ȣ���˵�����ɣ�
��2����AC��9cm��BC��6cmʱ����ͼ2����B���F����ֱ��l�Գƣ�����BF��CF����M��AC�ϣ���N��CF��һ�㣬�ֱ����M��N��MD��ֱ��l�ڵ�D��NE��ֱ��l�ڵ�E����M��A���������ÿ��1cm���ٶ���A��C·���˶����յ�ΪC����N�ӵ�F��������ÿ��3cm���ٶ���F��C��B��C��F·���˶����յ�ΪF����M��Nͬʱ��ʼ�˶������Դﵽ��Ӧ���յ�ʱֹͣ�˶������˶�ʱ��Ϊt�룮
������CMNΪ����ֱ��������ʱ����t��ֵ��
������MDC���CENȫ��ʱ����t��ֵ��

���𰸡���1����ACD���CBEȫ�ȣ����ɼ���������2���ٵ�t��![]() ���
���![]() ��ʱ����CMNΪ����ֱ�������Σ��ڵ�t��
��ʱ����CMNΪ����ֱ�������Σ��ڵ�t��![]() ���
���![]() ���
���![]() ��ʱ����MDC���CENȫ�ȣ�
��ʱ����MDC���CENȫ�ȣ�
��������
��1�����ݴ�ֱ�Ķ���õ���DAC=��ECB������AAS����֤����ACD�ա�CBE;
��2���ٷֵ�N��C��B·���˶��͵�N��B��C·���˶�������������ݵ��������εĶ����г���ʽ�����㼴�ɣ��ڷֵ�N��F��C·���˶�����N��C��B·���˶�����N��B��C·���˶�����N��C��F·���˶��������������ȫ�������ε��ж�������ʽ���㣮
��1����ACD���CBEȫ�ȣ��������£�
��AD��ֱ��l��
���DAC+��ACD��90�㣬
�ߡ�ACB��90�㣬
���BCE+��ACD��90�㣬
���DAC����ECB��
�ڡ�ACD�͡�CBE�У�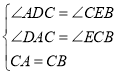 ��
��
���ACD�ա�CBE��AAS����
��2����������ã�AM��t��FN��3t��
��CM��8��t��
���۵������ʿ�֪��CF��CB��6��
��CN��6��3t��
��N��BC��ʱ����CMNΪ����ֱ�������Σ�
����N��C��B·���˶�ʱ��������ã�9��t��3t��6��
��ã�t��![]() ��
��
����N��B��C·���˶�ʱ��������ã�9��t��18��3t��
��ã�t��![]() ��
��
������������t��![]() ���
���![]() ��ʱ����CMNΪ����ֱ�������Σ�
��ʱ����CMNΪ����ֱ�������Σ�
�����۵������ʿ�֪����BCE����FCE��
�ߡ�MCD+��CMD��90�㣬��MCD+��BCE��90�㣬
���NCE����CMD��
�൱CM��CNʱ����MDC���CENȫ�ȣ�
����N��F��C·���˶�ʱ��9��t��6��3t��
��ã�t��![]() ���������⣩��
���������⣩��
����N��C��B·���˶�ʱ��9��t�T3t��6��
��ã�t��![]() ��
��
����N��B��C·���˶�ʱ��������ã�9��t��18��3t��
��ã�t��![]() ��
��
����N��C��F·���˶�ʱ��������ã�9��t��3t��18��
��ã�t��![]() ��
��
������������t��![]() ���
���![]() ���
���![]() ��ʱ����MDC���CENȫ�ȣ�
��ʱ����MDC���CENȫ�ȣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABD����AEC���ǵȱ������Σ�����BE��DC����O

(1)��֤��BE=DC ��
(2) ���DOB����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ������A��
������A��![]() ��0����B��
��0����B��![]() ��0��������y���ཻ�ڵ�C��
��0��������y���ཻ�ڵ�C��
��1�������������ߵı���ʽ��
��2�����ACB�Ķ�����
��3�����D�����������ߵ�һ������һ�㣬���ڶԳ�����Ҳ࣬��E���߶�AC�ϣ���DE��AC������DCE����AOC����ʱ�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ����Ƕ�֪��,![]()
���ǣ�-2x2+40x+5
=-2(x2-20x)+5
=-2(x2-20x+100)+200+5
=-2(x-10)2+205
����Ϊ![]() ������
������![]() ��
��![]()
���ԣ�-2x2+40x+5�����ֵ205.
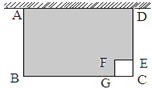
��ͼ��ijũ�����ó�34����դ��Χ��һ�߿�ǽ�ij�������ȦABCD��һ���߳�Ϊ1�������ι���CEFG.��AB=x��.
��1�����ú�x�Ĵ���ʽ��ʾBC�ij���ֱ��д�𰸣���
��2����ɽ����Χ��ͼ����Ӱ���ֵ����ΪS�����ú�x�Ĵ���ʽ��ʾS�������㵱x=5ʱS��ֵ��
��3�������ɽ����Χ���S�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������е��ش���̩������ⷿ������½���������ƻ�10���ڽ����������Ⱥ��ס�����⣬ǰ6�꣬ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף�����ʱ��x�Ĺ�ϵ��y=![]() x+5����x��λ���꣬1��x��6��xΪ����������4�꣬ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף�����ʱ��x�Ĺ�ϵ��y=-
x+5����x��λ���꣬1��x��6��xΪ����������4�꣬ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף�����ʱ��x�Ĺ�ϵ��y=-![]() x+
x+![]() ��x��λ���꣬7��x��10��xΪ������������ÿ��Ĺ��ⷿȫ�������꣮���⣬����������ǵ����ص�Ӱ�죬ÿ������Ҳ��֮�ϵ���Ԥ�ƣ���x��Ͷ��ʹ�õĹ��ⷿ�����z����λ��Ԫ/m2����ʱ��x����λ���꣬1��x��10��xΪ����������һ�κ�����ϵ���±���
��x��λ���꣬7��x��10��xΪ������������ÿ��Ĺ��ⷿȫ�������꣮���⣬����������ǵ����ص�Ӱ�죬ÿ������Ҳ��֮�ϵ���Ԥ�ƣ���x��Ͷ��ʹ�õĹ��ⷿ�����z����λ��Ԫ/m2����ʱ��x����λ���꣬1��x��10��xΪ����������һ�κ�����ϵ���±���
z��Ԫ/m2�� | 50 | 52 | 54 | 56 | 58 | �� |
x���꣩ | 1 | 2 | 3 | 4 | 5 | �� |
��1�����z��x�ĺ�����ϵʽ��
��2���������ڵڼ���Ͷ��Ĺ��ⷿ��ȡ�������࣬���Ϊ���ٰ���Ԫ��
��3������6�꿢��Ͷ��ʹ�õĹ��ⷿ�ɽ��20���˵�ס�����⣬�����ƻ��ڵ�10��Ͷ��Ĺ��ⷿ��������������£�Ҫ���˾�ס������ȵ�6���˾�ס��������a%�������ɽ��ס�����������ȵ�6�����1.35a%����a��ֵ��
���ο����ݣ�![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯һ���֪ʶ�����������涨��ÿ���༶��2��������2��Ů����1����������ʦ��ɴ����ӣ�������ʱ��ÿ��ֻ����3����Ա�ϳ���������������ʦ����μӣ�����2����Ա�ֱ���2��������2��Ů���и�������1����������1�����ɼס���2�������ͱ�����2��Ů����1������������˴����ӣ���ǡ�ó鵽�������ס�Ů��������λ������һ���ϳ������ĸ��ʣ�������������״ͼ�������б��������о����ȷ��������������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����߾�����A����1��0����B��4��0����C��0��2�����㣬��D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M��
��1���������������ʾ�Ķ��κ����ı���ʽ��
��2����֪��F��0��![]() ��������P��x�����˶�ʱ������mΪ��ֵʱ���ı���DMQF��ƽ���ı��Σ�
��������P��x�����˶�ʱ������mΪ��ֵʱ���ı���DMQF��ƽ���ı��Σ�
��3����P���߶�AB�˶������У��Ƿ���ڵ�Q��ʹ���Ե�B��Q��MΪ��������������BOD���ƣ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A1��A2��A3��B1��B2��B3�ֱ���ֱ��y=![]() ��x���ϣ���OA1B1����B1A2B2����B2A3B3���ǵ���ֱ�������Σ���A3������Ϊ_______.
��x���ϣ���OA1B1����B1A2B2����B2A3B3���ǵ���ֱ�������Σ���A3������Ϊ_______.
 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
��![]() ��
��![]() ��
��![]() .
.![]() ��ƽ���߷ֱ�
��ƽ���߷ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ���㣬
���㣬![]() Ϊ
Ϊ![]() ���е㣬�ӳ�
���е㣬�ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() .���н��ۣ���
.���н��ۣ���![]() ����
����![]() ����
����![]() �ǵ��������Σ���
�ǵ��������Σ���![]() .������ȷ�Ľ��۸����ǣ� ��
.������ȷ�Ľ��۸����ǣ� ��

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com