Question

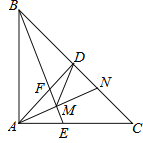
【题目】如图，等腰中，，于.的平分线分别交，于点，两点，为的中点，延长交于点，连接.下列结论：①；②；③是等腰三角形；④.其中正确的结论个数是（ ）

A.1个B.2个C.3个D.4个

Answer 1

【答案】D

【解析】

求出BD=AD，∠DBF=∠DAN，∠BDF=∠ADN，证△DFB≌△DAN，即可判断①，证△ABF≌△CAN，推出CN=AF=AE，即可判断②；根据A、B、D、M四点共圆求出∠ADM=22.5°，即可判断④，根据三角形外角性质求出∠DNM，求出∠MDN=∠DNM，即可判断③．

∵∠BAC=90°，AC=AB，AD⊥BC，
∴∠ABC=∠C=45°，AD=BD=CD，∠ADN=∠ADB=90°，
∴∠BAD=45°=∠CAD，
∵BE平分∠ABC，
∴∠ABE=∠CBE=∠ABC=22.5°，
∴∠BFD=∠AEB=90°-22.5°=67.5°，
∴∠AFE=∠BFD=∠AEB=67.5°，
∴AF=AE，
∵M为EF的中点，
∴AM⊥BE，

∴∠AMF=∠AME=90°，
∴∠DAN=90°-67.5°=22.5°=∠MBN，
在△FBD和△NAD中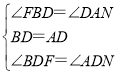

∴△FBD≌△NAD，
∴DF=DN，∴①正确；
在△AFB和△△CNA中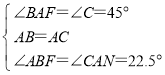

∴△AFB≌△CAN，
∴AF=CN，
∵AF=AE，
∴AE=CN，∴②正确；
∴A、B、D、M四点共圆，
∴∠ABM=∠ADM=22.5°，
∴∠DMN=∠DAN+∠ADM=22.5°+22.5°=45°，∴④正确；
∵∠DNA=∠C+∠CAN=45°+22.5°=67.5°，
∴∠MDN=180°-45°-67.5°=67.5°=∠DNM，
∴DM=MN，∴△DMN是等腰三角形，∴③正确；
即正确的有4个，
故选：D．