Question

【题目】中，.设的面积为.

①图1中，为中点，，，，是上的四点；

②图2中，，，，，，，交于点；

③图3中，，D为中点，.

其中，阴影部分面积为的是______（填序号）.

Answer 1

【答案】①②③．

【解析】

由等腰三角形的性质可判断①，由等边三角形的性质可判断②，由ASA可证△ADF≌△DBE，可得S△ADF=S△DBE，即可判断③．

如图1，∵AB=AC，点D是BC中点，
∴BD=CD，AD垂直平分BC，
∴S△BDN=S△DCN，S△BMN=S△MNC，S△BFM=S△CFM，S△EFB=S△EFC，S△AEB=S△AEC，
∴阴影部分面积为S；
如图2，∵AB=AC，∠BAC=60°，
∴△ABC是等边三角形，且AD⊥BC，BE⊥AC，CF⊥AB，
∴AD垂直平分BC，BE垂直平分AC，CF垂直平分AB，
∴S△BDO=S△CDO，S△AEO=S△CEO，S△AFO=S△BFO，
∴阴影部分面积为S；
如图3，连接AD，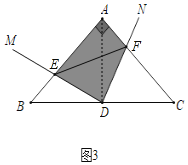

∵AB=AC，∠BAC=90°，D为BC中点，
∴AD=BD，∠B=∠DAC=45°，AD⊥BC，
∴∠ADM+∠BDM=90°，且∠MDA+∠ADN=90°，
∴∠BDM=∠ADN，且AD=BD，∠B=∠DAC=45°，
∴△ADF≌△DBE（ASA）
∴S△ADF=S△DBE，
∴阴影部分面积为S；
故答案为：①②③．