
【题目】如图,四边形ABCD是正方形,直线a,b,c分别通过A、D、C三点,且a∥b∥c.若a与b之间的距离是5,b与c之间的距离是7,则正方形ABCD的面积是( )

A.70B.74C.144D.148
【答案】B
【解析】
过A作AM⊥直线b于M,过D作DN⊥直线c于N,求出∠AMD=∠DNC=90°,AD=DC,∠1=∠3,根据AAS推出△AMD≌△CND,根据全等得出AM=CN,求出AM=CN=5,DN=7,在Rt△DNC中,由勾股定理求出DC2即可.
解:如图:
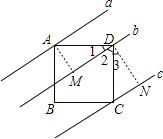
过A作AM⊥直线b于M,过D作DN⊥直线c于N,
则∠AMD=∠DNC=90°,
∵直线b∥直线c,DN⊥直线c,
∴∠2+∠3=90°,
∵四边形ABCD是正方形,
∴AD=DC,∠1+∠2=90°,
∴∠1=∠3,
在△AMD和△CND中
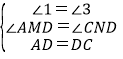
∴△AMD≌△CND,
∴AM=CN,
∵a与b之间的距离是5,b与c之间的距离是7,
∴AM=CN=5,DN=7,
在Rt△DNC中,由勾股定理得:DC2=DN2+CN2=72+52=74,
即正方形ABCD的面积为74,
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知点D,E,F分别为BC,AD,AE的中点,且S△ABC=4cm2,则阴影部分面积S=( )cm2.
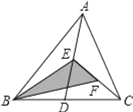
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() .设
.设![]() 的面积为
的面积为![]() .
.

①图1中,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的四点;
上的四点;
②图2中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 交于点
交于点![]() ;
;
③图3中,![]() ,D为
,D为![]() 中点,
中点,![]() .
.
其中,阴影部分面积为![]() 的是______(填序号).
的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知RtΔABC,∠C=90°,D为BC的中点.以AC为直径的圆O交AB于点E.
(1)求证:DE是圆O的切线.
(2)若AE:EB=1:2,BC=6,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABE中,∠BAE=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )

A. 45°B. 60°C. 50°D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
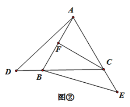
【题目】如图,△ABC是等边三角形,点D、E分别是直线BC、AC上的点,且BD=CE.
(1)如图①,当点D、E分别在线段BC、AC上时,BE与AD相交于点F.求∠AFB的度数.
(2)如图②,当点D在CB的延长线上,点E在AC的延长线上时,CF为△ABC的高线则线段CD、AF、CE、之间的数量关系是 ,并加以证明.
(3)在①的条件下,连接FC,如图③,若∠DFC=90°,AF= 3![]() ,求BF的长.
,求BF的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC的边AB,AC的外侧分别作等边△ABD和等边△ACE,连接DC,BE.
(1)求证:DC=BE;
(2)若BD=3,BC=4, BD⊥BC于点B,请求出△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com