
【题目】在△ABC中,∠ACB=45°,点D为射线BC上一动点(与点B、C不重合),连接AD,以AD为一边在AD一侧作正方形ADEF(如图1).
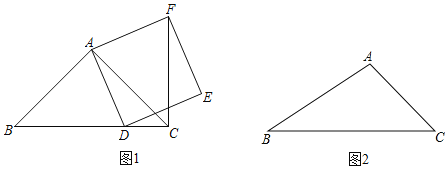
(1)如果AB=AC,且点D在线段BC上运动,证明:CF⊥BD;
(2)如果AB≠AC,且点D在线段BC的延长线上运动,请在图2中画出相应的示意图,此时(1)中的结论是否成立?请说明理由;
(3)设正方形ADEF的边DE所在直线与直线CF相交于点P,若AC=4,CD=2,求线段CP的长.
【答案】(1)见解析;(2)AB≠AC时,CF⊥BD的结论成立.理由见解析;(3)线段CP的长为2﹣![]() 或2+
或2+![]() .
.
【解析】
(1)证出∠BAC=∠DAF=90°,得出∠BAD=∠CAF;可证△DAB≌△FAC(SAS),得∠ACF=∠ABD=45°,得出∠BCF=∠ACB+∠ACF=90°.即CF⊥BD.
(2)过点A作AG⊥AC交BC于点G,可得出AC=AG,易证△GAD≌△CAF(SAS),得出∠ACF=∠AGD=45°,∠BCF=∠ACB+∠ACF=90°.即CF⊥BD.
(3)分两种情况去解答.①点D在线段BC上运动,求出AQ=CQ=4.即DQ=4﹣2=2,易证△AQD∽△DCP,得出对应边成比例,即可得出CP=![]() ;②点D在线段BC延长线上运动时,同理得出CP=
;②点D在线段BC延长线上运动时,同理得出CP=![]() .
.
(1)证明:∵四边形ADEF是正方形,
∴∠DAF=90°,AD=AF,
∵AB=AC,∠BAC=90°,
∴∠BAD+∠DAC=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,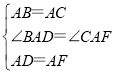 ,
,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°
∵AB=AC,∠BAC=90°,
∴∠ACB=∠ABD=45°
∴∠BCF=∠ACB+∠ACF=90°,
∴CF⊥BD;
(2)解:如图2所示:AB≠AC时,CF⊥BD的结论成立.理由如下:
过点A作GA⊥AC交BC于点G,
则∠GAD=∠CAF=90°+∠CAD,
∵∠ACB=45°,
∴∠AGD=45°,
∴AC=AG,
在△GAD和△CAF中,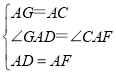 ,
,
∴△GAD≌△CAF(SAS),
∴∠ACF=∠AGD=45°,
∴∠BCF=∠ACB+∠ACF=90°,
∴CF⊥BD;
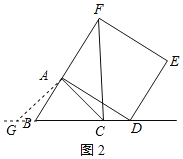
(3)解:过点A作AQ⊥BC交CB的延长线于点Q,
①点D在线段BC上运动时,如图3所示:
∵∠BCA=45°,
∴△ACQ是等腰直角三角形,
∵AC=4
∴AQ=CQ=![]() AC=
AC=![]() .
.
∴DQ=CQ﹣CD=![]() ﹣2,
﹣2,
∵AQ⊥BC,∠ADE=90°,
∴∠DAQ+∠ADQ=∠ADQ+∠PDC=90°,
∴∠DAQ=∠PDC,
∵∠AQD=∠DCP=90°,
∴△DCP∽△AQD,
∴![]() ,即
,即![]() ,
,
解得:CP=2﹣![]() ;
;
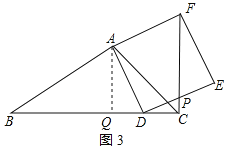
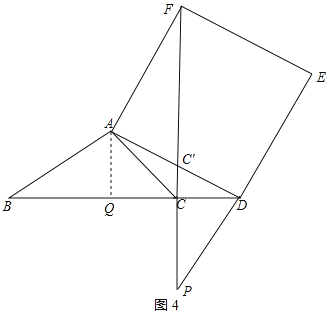
②点D在线段BC延长线上运动时,如图4所示:
∵∠BCA=45°,
∴AQ=CQ=![]() ,
,
∴DQ=AQ+CD=![]() +2.
+2.
∵AQ⊥BC于Q,
∴∠Q=∠FAD=90°,
∵∠C′AF=∠C′CD=90°,∠AC′F=∠CC′D,
∴∠ADQ=∠AFC′,
则△AQD∽△AC′F.
∴CF⊥BD,
∴△AQD∽△DCP,
∴![]() ,即
,即![]() ,
,
解得:CP=![]() ,
,
综上所述,线段CP的长为![]() 或
或![]() .
.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
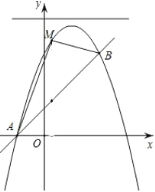
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() :
:![]() 相交于
相交于![]() 和点
和点![]() 两点.
两点.
⑴求抛物线![]() 的函数表达式;
的函数表达式;
⑵若点![]() 是位于直线
是位于直线![]() 上方抛物线上的一动点,以
上方抛物线上的一动点,以![]() 为相邻两边作平行四边形
为相邻两边作平行四边形![]() ,当平行四边形
,当平行四边形![]() 的面积最大时,求此时四边形
的面积最大时,求此时四边形![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
⑶在抛物线![]() 的对称轴上是否存在定点
的对称轴上是否存在定点![]() ,使抛物线
,使抛物线![]() 上任意一点
上任意一点![]() 到点
到点![]() 的距离等于到直线
的距离等于到直线![]() 的距离,若存在,求出定点
的距离,若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:

(1)求本次比赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意;B级:满意;C级:基本满意;D级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
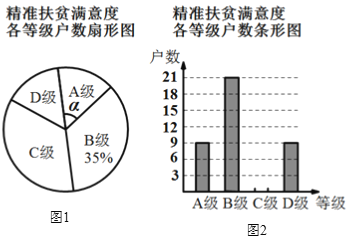
(1)本次抽样调查测试的建档立卡贫困户的总户数______.
(2)图1中,∠α的度数是______,并把图2条形统计图补充完整.
(3)某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的人数约为多少户?
(4)调查人员想从5户建档立卡贫困户(分别记为![]() )中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户
)中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABMN中,AN=1,点C是MN的中点,分別连接AC,BC,且BC=2,点D为AC的中点,点E为边AB上一个动点,连接DE,点A关于直线DE的对称点为点F,分别连接DF,EF.当EF⊥AC时,AE的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
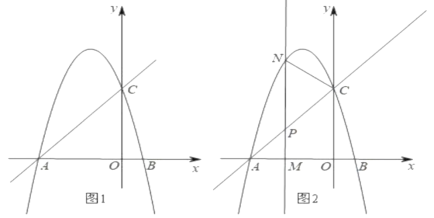
【题目】如图1,直线y=x+c与x轴交于点A(-3,0),与y轴交于点C,抛物线y=-x2+bx+c经过点A、C.
(1)求抛物线的解析式;
(2)如图2所示,M是线段0A上一个动点,过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N.若以C、P、N为顶点的三角形与△APM相似,求四边形MNCO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
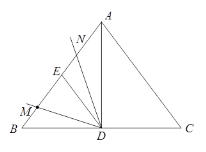
【题目】如图,在![]() 中,
中,![]() cm,
cm,![]() cm,点
cm,点![]() 为
为![]() 的中点,点E为AB的中点.点
的中点,点E为AB的中点.点![]() 为AB边上一动点,从点B出发,运动到点A停止,将射线DM绕点
为AB边上一动点,从点B出发,运动到点A停止,将射线DM绕点![]() 顺时针旋转
顺时针旋转![]() 度(其中
度(其中![]() ),得到射线DN,DN与边AB或AC交于点N.设
),得到射线DN,DN与边AB或AC交于点N.设![]() 、
、![]() 两点间的距离为
两点间的距离为![]() cm,
cm,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() cm.
cm.
小涛根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小涛的探究过程,请补充完整.
(1)列表:按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() 与
与![]() 的几组对应值:
的几组对应值:
x/cm | 0 | 0.3 | 0.5 | 1.0 | 1.5 | 1.8 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 4.8 | 5.0 |
y/cm | 2.5 | 2.44 | 2.42 | 2.47 | 2.79 | 2.94 | 2.52 | 2.41 | 2.48 | 2.66 | 2.9 | 3.08 | 3.2 |
请你通过测量或计算,补全表格;
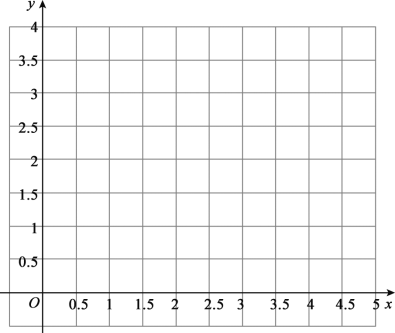
(2)描点、连线:在平面直角坐标系![]() 中,描出补全后的表格中各组数值所对应的点
中,描出补全后的表格中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 关于
关于![]() 的图象.
的图象.
(3)结合函数图象,解决问题:当![]() 时,
时,![]() 的长度大约是 cm.(结果保留一位小数)
的长度大约是 cm.(结果保留一位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com