
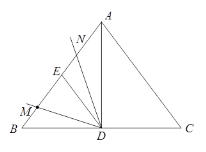
����Ŀ����ͼ����![]() �У�
��![]() cm��
cm��![]() cm����
cm����![]() Ϊ
Ϊ![]() ���е㣬��EΪAB���е㣮��
���е㣬��EΪAB���е㣮��![]() ΪAB����һ���㣬�ӵ�B�������˶�����Aֹͣ��������DM�Ƶ�
ΪAB����һ���㣬�ӵ�B�������˶�����Aֹͣ��������DM�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() �ȣ�����
�ȣ�����![]() �����õ�����DN��DN���AB��AC���ڵ�N����
�����õ�����DN��DN���AB��AC���ڵ�N����![]() ��
��![]() �����ľ���Ϊ
�����ľ���Ϊ![]() cm��
cm��![]() ��
��![]() �����ľ���Ϊ
�����ľ���Ϊ![]() cm��
cm��
С�θ���ѧϰ�����ľ��飬�Ժ���![]() ���Ա���
���Ա���![]() �ı仯���仯�Ĺ��ɽ�����̽����
�ı仯���仯�Ĺ��ɽ�����̽����
������С�ε�̽�����̣��벹��������
��1���б��������±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���![]() ��
��![]() �ļ����Ӧֵ��
�ļ����Ӧֵ��
x/cm | 0 | 0.3 | 0.5 | 1.0 | 1.5 | 1.8 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 4.8 | 5.0 |
y/cm | 2.5 | 2.44 | 2.42 | 2.47 | 2.79 | 2.94 | 2.52 | 2.41 | 2.48 | 2.66 | 2.9 | 3.08 | 3.2 |
����ͨ����������㣬��ȫ����
��2����㡢���ߣ���ƽ��ֱ������ϵ![]() �У������ȫ��ı����и�����ֵ����Ӧ�ĵ�
�У������ȫ��ı����и�����ֵ����Ӧ�ĵ�![]() ������������
������������![]() ����
����![]() ��ͼ��
��ͼ��
��3����Ϻ���ͼ������⣺��![]() ʱ��
ʱ��![]() �ij��ȴ�Լ���� ��cm�����������һλС����
�ij��ȴ�Լ���� ��cm�����������һλС����
���𰸡���1��3.2����2�������������3��1.7��1.9��4.7
��������
��1��֤����BMD=90������y=MN=MDtan��=��DBsin����tan��=2.4��![]() =3.2��
=3.2��
��2����㡢���ߵú���ͼ��
��3����MN=BDʱ����y=3����ͼ��x��ֵ���ɣ�
�⣺��1��x=BM=1.8��
��ΪAB=AC=5,BC=6,DΪBC���е㣬
��BD=DC=3,AD��BC.
��cos��B=![]() ��tan��B=
��tan��B=![]() .
.
�ڡ�MBD�У�BD=3����cosB=cos����tan��=![]() ��
��
����M��MH��BD�ڵ�H��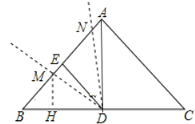
��BH=BMcos��=1.8��![]() =1.08��ͬ��MH=1.44��
=1.08��ͬ��MH=1.44��
HD=BD-BH=3-1.08=1.92��
MD=![]() =2.4��
=2.4��
��BD2=BM2+MD2��
�ʡ�BMD=90����
��ֱ��������ABD�У�E��AB���е㣬
��BE=ED.
���B=��BDE.
�֡ߡ�B=��MDN.
���MDN=��B=��.
��y=MN=MDtan�� =2.4��![]() =3.2��
=3.2��
��ȫ�ı����������£�
x/cm | 0 | 0.3 | 0.5 | 1.0 | 1.5 | 1.8 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 4.8 | 5.0 |
y/cm | 2.5 | 2.44 | 2.42 | 2.47 | 2.79 | 3.2 | 2.94 | 2.52 | 2.41 | 2.48 | 2.66 | 2.9 | 3.08 | 3.2 |
��2����㡢���ߵõ����º���ͼ��
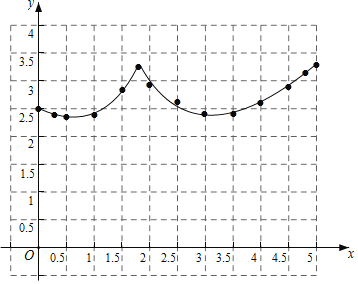
��3����MN=BDʱ����y=3����ͼ��x��BM�ij��ȴ�Լ��1.7��1.9��4.7��
�ʴ�Ϊ��1.7��1.9��4.7�������ֵ���²�0.1����ԣ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���ACB��45�㣬��DΪ����BC��һ���㣨���B��C���غϣ�������AD����ADΪһ����ADһ����������ADEF����ͼ1����
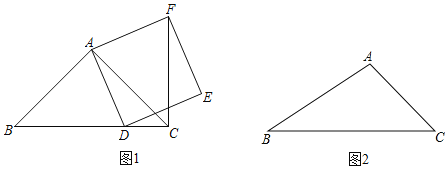
��1�����AB��AC���ҵ�D���߶�BC���˶���֤����CF��BD��
��2�����AB��AC���ҵ�D���߶�BC���ӳ������˶�������ͼ2�л�����Ӧ��ʾ��ͼ����ʱ��1���еĽ����Ƿ��������˵�����ɣ�
��3����������ADEF�ı�DE����ֱ����ֱ��CF�ཻ�ڵ�P����AC��4��CD��2�����߶�CP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ҹ�����ط����صġ����顱��Ϊ�˹��������Լ��ˮ���������ƻ�ʵ�������շ��ƣ���ÿ����ˮ��������14�֣���14�֣�ʱ��ÿ�ְ����������Żݼ��շѣ�ÿ�³���14��ʱ����������ÿ�ְ��г����ڼ��շѣ�СӢ��1�·���ˮ20�֣���ˮ��29Ԫ��2�·���ˮ18�֣���ˮ��24Ԫ��
��1����ÿ��ˮ�����������Żݼۺ��г����ڼ۷ֱ��Ƕ��٣�
��2����ÿ����ˮ��Ϊx�֣�Ӧ��ˮ��ΪyԪ��д��y��x֮��ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����������������������ù������г����ﳵʱ��t����λ���֣�������õ����ݷֳ����飬����������ͳ��ͼ�������ͼ����Ϣ������������⣺
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922393511583744/1923977001213952/STEM/d5900c7cb9b84a9a89aefef7d82bcf93.png]
��1����α�������������Ƕ��٣�
��2�������ʾA�������Բ�ĽǵĶ���������ȫ����ͳ��ͼ��
��3����������г���ƽ���ٶ�Ϊ12km/h������㣬�����ù������г��������У��ﳵ·�̲�����6km��������ռ�İٷֱȡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ŀ������ͼ1��ƽ���ϣ�����������һ��Ϊ12 ����Ϊ6 �ľ��Σ��������������ε��ڲ����߽�ͨ����ת����ƽ�ƻ���ת���ķ�ʽ�����ɵشӺ����ת�����ţ��������α߳�����С����![]() �����ס��ҡ�����������Ϊ�߳���С�������Σ�������ñ߳�
�����ס��ҡ�����������Ϊ�߳���С�������Σ�������ñ߳�![]() ����ȡ��С����
����ȡ��С����![]() ��
��
�ף���ͼ2��˼·�ǵ�![]() Ϊ���ζԽ��߳�ʱ�Ϳ���ת��ȥ�����ȡn=14��
Ϊ���ζԽ��߳�ʱ�Ϳ���ת��ȥ�����ȡn=14��
�ң���ͼ3��˼·�ǵ�![]() Ϊ�������Բֱ����ʱ�Ϳ���ת��ȥ�����ȡn=14��
Ϊ�������Բֱ����ʱ�Ϳ���ת��ȥ�����ȡn=14��
������ͼ4��˼·�ǵ�![]() Ϊ���εij����֮�͵�
Ϊ���εij����֮�͵�![]() ��ʱ�Ϳ���ת��ȥ�����ȡn=13��
��ʱ�Ϳ���ת��ȥ�����ȡn=13��
�ס��ҡ�����˼·�ͽ������ȷ����___________ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������y��k1x�뷴��������y��![]() ��ͼ���ཻ��A��B���㣬AC��x���ڵ�C��CD��AB��y���ڵ�D������AD��BD����S��ABD��6�������н�����ȷ���ǣ�������
��ͼ���ཻ��A��B���㣬AC��x���ڵ�C��CD��AB��y���ڵ�D������AD��BD����S��ABD��6�������н�����ȷ���ǣ�������
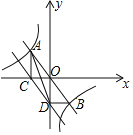
A.k1����6B.k1����3C.k2����6D.k2����12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��E��x0��yo������F��x2��y2������M��x1��y1�����߶�EF���е㣬��x1��![]() ��y1��
��y1��![]() ����ƽ��ֱ������ϵ����������A��1����1����B����1����1����C��0��1������P��0��2�����ڵ�A�ĶԳƵ�P1����P��A��P1���㹲�ߣ���PA��P1A����P1���ڵ�B�ĶԳƵ�P2��P2���ڵ�C�ĶԳƵ�P3�������˹��ɼ�����A��B��C����Ϊ�ԳƵ��ظ�ǰ��IJ��������εõ���P4��P5��P6�������P2020�������ǣ�������
����ƽ��ֱ������ϵ����������A��1����1����B����1����1����C��0��1������P��0��2�����ڵ�A�ĶԳƵ�P1����P��A��P1���㹲�ߣ���PA��P1A����P1���ڵ�B�ĶԳƵ�P2��P2���ڵ�C�ĶԳƵ�P3�������˹��ɼ�����A��B��C����Ϊ�ԳƵ��ظ�ǰ��IJ��������εõ���P4��P5��P6�������P2020�������ǣ�������
A.��4��0��B.����2��2��C.��2����4��D.����4��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����߾�����A����1��0����B��4��0����C��0��2�����㣬��D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M��
��1���������������ʾ�Ķ��κ����ı���ʽ��
��2����֪��F��0��![]() ��������P��x�����˶�ʱ������mΪ��ֵʱ���ı���DMQF��ƽ���ı��Σ�
��������P��x�����˶�ʱ������mΪ��ֵʱ���ı���DMQF��ƽ���ı��Σ�
��3����P���߶�AB�˶������У��Ƿ���ڵ�Q��ʹ���Ե�B��Q��MΪ��������������BOD���ƣ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019�������й�����70���꣬�ڡ���ף���й�����70�껪�������������£�����ijѧУ��֯��չ�˷ḻ��ʵĻ��������ˡ�A��ʫ������չ�ݣ�B��������ݣ�C���黭��Ʒչ����D���ֹ���Ʒչ�����ĸ�ר����ÿ��ѧ����ѡһ��ר�����룮Ϊ�˽���չ�����ѧУ�����ȡ�˲���ѧ�����е��飬�����ݵ�������������ͼ��ʾ�IJ�����������ͳ��ͼ������ͳ��ͼ��
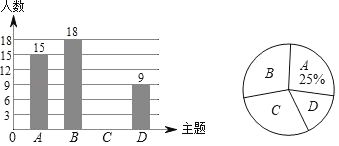
��1��������������ѧ���������� ���ˣ�
��2�����㲹ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У���B���������ε�Բ�Ľ�Ϊ�� ���ȣ�
��4��С�κ�С����������������е�һ��ר���������û���״ͼ���б��ķ�ʽ������ǡ��ѡ��ͬһ��ר���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com