练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一如图，在△ABC中，AB=41cm，BC=18cm，BC边上的中线AD=40cm．△ABC是等腰三角形吗？为什么？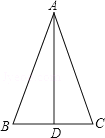

    【答案】解：△ABC是等腰三角形，
    理由是：∵BC=18cm，BC边上的中线为AD，
    ∴BD=CD=9cm
    ∵AB=41cm，BC=18cm，AD=40cm
    ∴AB2=1681，
    BD2+AD2=1681，
    ∴AB2=BD2+AD2 ，
    ∴AD⊥BC
    ∵BD=CD，
    ∴AC=AB
    ∴△ABC是等腰三角形．
    【解析】由已知可得BD的长，再根据勾股定理的逆定理可判定AD垂直BC，从而根据可利用勾股定理求得AC的长，此时发现AB=AC，即该三角形是等腰三角形．此题主要考查学生对勾股定理的逆定理及等腰三角形的判定线段的垂直平分线性质的理解及运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】二次函数y＝(x+2)2＋3的图象的顶点坐标是______。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知数轴上有三点A、B、C，AB=60，点A对应的数是40．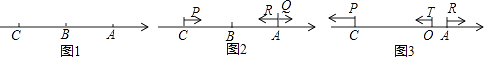
    （1）若BC：AC=4：7，求点C到原点的距离；
    （2）如图2，在（1）的条件下，动点P、Q两点同时从C、A出发向右运动，同时动点R从点A向左运动，已知点P的速度是点R的速度的3倍，点Q的速度是点R的速度2倍少5个单位长度/秒．经过5秒，点P、Q之间的距离与点Q、R之间的距离相等，求动点Q的速度；
    （3）如图3，在（1）的条件下，O表示原点，动点P、T分别从C、O两点同时出发向左运动，同时动点R从点A出发向右运动，点P、T、R的速度分别为5个单位长度/秒、1个单位长度/秒、2个单位长度/秒，在运动过程中，如果点M为线段PT的中点，点N为线段OR的中点．请问PT﹣MN的值是否会发生变化？若不变，请求出相应的数值；若变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对一个图形进行放缩时，下列说法中正确的是（　　）.
    A.图形中线段的长度与角的大小都保持不变
    B.图形中线段的长度与角的大小都会改变
    C.图形中线段的长度保持不变、角的大小可以改变
    D.图形中线段的长度可以改变、角的大小保持不变

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】开州区城区2018年底已有绿化面积700公顷，响应“青山绿水就是金山银山”的号召，绿化面积逐年增加，预计到2020年底 绿化面积增加到1000公顷，设绿化面积平均每年的增长率为x，由题意，所列方程正确的是( )

    A.700(1＋x)＝1000B.700(1＋x)2＝1000

    C.700(1＋2x)＝1000D.1000(1－x)2＝700

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】当a、b、c为何值时，代数式 有最小值？并求出这个最小值和此时以a、b、c值为边的三角形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据直角三角形的判定的知识解决下列问题
    （1）如图①所示，P是等边△ABC内的一点，连接PA、PB、PC，将△BAP绕B点顺时针旋转60°得△BCQ，连接PQ．若PA2+PB2=PC2，证明∠PQC=90°；

    （2）如图②所示，P是等腰直角△ABC（∠ABC=90°）内的一点，连接PA、PB、PC，将△BAP绕B点顺时针旋转90°得△BCQ，连接PQ．当PA、PB、PC满足什么条件时，∠PQC=90°？请说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对某班40同学的一次数学成绩进行统计，适当分组后80～90分这个分数段的划记人数为“”，那么此班在这个分数段的人数占全班人数的百分比是（　　）
    A.20%
    B.40%
    C.8%
    D.25%

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将直角三角形ABC沿AB方向平移AD距离得到直角三角形DEF．已知BE=4cm，EF=7cm，CG=3cm，求图中阴影部分的面积．

    查看答案和解析>>

    同步练习册答案