
如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.
(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.(提示:过点P作PE∥l1)
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?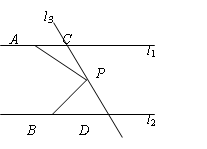
(1)∠APB=∠PAC+∠PBD;(2)∠PBD=∠PAC+∠APB,或∠PAC=∠PBD+∠APB.
解析试题分析:(1)当P点在C、D之间运动时,首先过点P作PE∥l1,由l1∥l2,可得PE∥l2∥l1,根据两直线平行,内错角相等,即可求得:∠APB=∠PAC+∠PBD.
(2)当点P在C、D两点的外侧运动时,由直线l1∥l2,根据两直线平行,同位角相等与三角形外角的性质,即可求得:∠PBD=∠PAC+∠APB.
试题解析:(1)如图①,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)如图②,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
如图③,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:
∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
考点:平行线的性质.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题
已知:如图,直线AB与直线BC相交于点B,点D是直线BC上一点,求作:点E,使直线DE∥AB,且点E到B、D两点的距离相等.(尺规作图,要求在题目的原图中完成作图)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知∠AOB, OE平分∠AOC, OF平分∠BOC.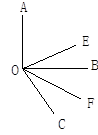
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数;
(2)猜想∠EOF与∠AOB的数量关系;
(3)若∠AOB+∠EOF=156°,则∠EOF是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平行四边形ABCD中,AD>AB.
(1)作出∠ABC的平分线(尺规作图,保留作图痕迹,不写作法);
(2)若(1)中所作的角平分线交AD于点E,AF⊥BE,垂足为点O,交BC于点F,连接EF.求证:四边形ABFE为菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com