
如图,在平行四边形ABCD中,AD>AB.
(1)作出∠ABC的平分线(尺规作图,保留作图痕迹,不写作法);
(2)若(1)中所作的角平分线交AD于点E,AF⊥BE,垂足为点O,交BC于点F,连接EF.求证:四边形ABFE为菱形.
解:(1)如图所示:
(2)首先根据角平分线的性质以及平行线的性质得出∠ABE=∠AEB,进而得出△ABO≌△FBO,进而利用AF⊥BE,BO=EO,AO=FO,得出即可。
解析分析:(1)根据角平分线的作法作出∠ABC的平分线即可。
(2)首先根据角平分线的性质以及平行线的性质得出∠ABE=∠AEB,进而得出△ABO≌△FBO,进而利用AF⊥BE,BO=EO,AO=FO,得出即可。
解:(1)如图所示:
(2)证明:∵BE平分∠ABC,∴∠ABE=∠EAF。
∵∠EBF=∠AEB,∴∠ABE=∠AEB。∴AB=AE。
∵AO⊥BE,∴BO=EO。
∵在△ABO和△FBO中,∠ABO=∠FBO ,BO=EO,∠AOB=∠FOB,
∴△ABO≌△FBO(ASA)。∴AO=FO。
∵AF⊥BE,BO=EO,AO=FO。∴四边形ABFE为菱形。


科目:初中数学 来源: 题型:解答题
如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.
(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.(提示:过点P作PE∥l1)
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?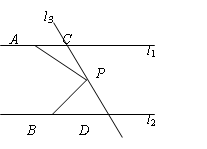
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在梯形ABCD中,AB∥DC,∠B=90°,且AB=10,BC=6,CD=2.点E从点B出发沿BC方向运动,过点E作EF∥AD交边AB于点F.将△BEF沿EF所在的直线折叠得到△GEF,直线FG、EG分别交AD于点M、N,当EG过点D时,点E即停止运动.设BE=x,△GEF与梯形ABCD的重叠部分的面积为y.
(1)证明△AMF是等腰三角形;
(2)当EG过点D时(如图(3)),求x的值;
(3)将y表示成x的函数,并求y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
以下是甲、乙、丙三人看地图时对四个坐标的描述:
甲:从学校向北直走500米,再向东直走100米可到图书馆.
乙:从学校向西直走300米,再向北直走200米可到邮局.
丙:邮局在火车站西200米处.
根据三人的描述,若从图书馆出发,判断下列哪一种走法,其终点是火车站( )
| A.向南直走300米,再向西直走200米 |
| B.向南直走300米,再向西直走100米 |
| C.向南直走700米,再向西直走200米 |
| D.向南直走700米,再向西直走600米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com