
【题目】如图,PA、PB、CD分别切⊙O于A、B、E,CD交PA、PB于C、D两点,若∠P=40°,则∠PAE+∠PBE的度数为( )

A. 50° B. 62° C. 66° D. 70°
【答案】D
【解析】
由PA、PB、CD分别切⊙O于A、B、E,CD交PA、PB于C、D两点,根据切线长定理即可得:CE=CA,DE=DB,然后由等边对等角与三角形外角的性质,可求得∠PAE= ![]() ∠PCD,∠PBE=
∠PCD,∠PBE= ![]() ∠PDC,继而求得∠PAE+∠PBE的度数.
∠PDC,继而求得∠PAE+∠PBE的度数.
∵PA、PB、CD分别切⊙O于A. B.E,CD交PA、PB于C.D两点,
∴CE=CA,DE=DB,
∴∠CAE=∠CEA,∠DEB=∠DBE,
∴∠PCD=∠CAE+∠CEA=2∠CAE,∠PDC=∠DEB+∠DBE=2∠DBE,
∴∠CAE=![]() ∠PCD,∠DBE=
∠PCD,∠DBE=![]() ∠PDC,
∠PDC,
即∠PAE=![]() ∠PCD,∠PBE=
∠PCD,∠PBE=![]() ∠PDC,
∠PDC,
∵∠P=40![]() ,
,
∴∠PAE+∠PBE=![]() ∠PCD+
∠PCD+![]() ∠PDC=
∠PDC=![]() (∠PCD+∠PDC)=
(∠PCD+∠PDC)=![]() (180
(180![]() ∠P)=70
∠P)=70![]() .
.
故答案选:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
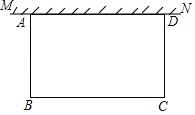
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知经过原点的抛物线![]() 与
与![]() 轴的另一个交点为
轴的另一个交点为![]() ,现将抛物线向右平移
,现将抛物线向右平移![]() 个单位长度,所得抛物线与
个单位长度,所得抛物线与![]() 轴交于
轴交于![]() ,与原抛物线交于点
,与原抛物线交于点![]() ,设
,设![]() 的面积为
的面积为![]() ,则用
,则用![]() 表示
表示![]() =__________
=__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC切⊙O于点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F.

(1)试判断∠CBD与∠CEB是否相等,并证明你的结论;
(2)求证:![]() ;
;
(3)若BC=![]() AB,求tan∠CDF的值.
AB,求tan∠CDF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
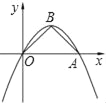
【题目】如图,抛物线y=ax2+bx经过点A(4,0)、B(2,2),连接OB、AB.
(1)求抛物线的解析式;
(2)求证:△OAB是等腰直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com