
科目:初中数学 来源: 题型:
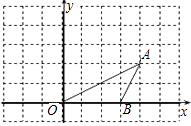 90°得到△OA′B′.
90°得到△OA′B′.查看答案和解析>>
科目:初中数学 来源: 题型:
 |
| AB |
| 1 |
| 3 |
 |
| AB |
| 19 |
| 3 |
| 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 |
| 3 |
| 4 |
| 3 |
3+
| ||
| 2 |
3+
| ||
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 O按逆时针方向旋转90°得到△OA′B′.
O按逆时针方向旋转90°得到△OA′B′.查看答案和解析>>
科目:初中数学 来源:2012年江苏省丹阳市初二数学质量检测试卷数学试卷(解析版) 题型:解答题
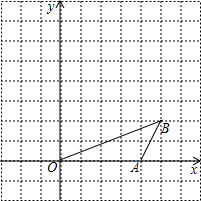
如图,在正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).

(1)以点O(0,0)为位似中心,按比例尺3:1在位似中心的同侧将△OAB放大为△OA’B’,放大后点A、B的对应点分别为A’、B’ .画出△OA’B’,并写出点A’、B’的坐标:A’( ),B’( ).
(2)在(1)中,若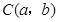 为线段
为线段 上任一点,写出变化后点
上任一点,写出变化后点 的对应点
的对应点 的坐标
( ).
的坐标
( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com