
����Ŀ���ڡ������ͥ�ա�ǰϦ��ijУ��ί�����ȡ��n����Уѧ�����ԡ������ͥ�ա�������ϲ���ļ�ͥ���ʽ�����ʾ����飮�ʾ��еļ�ͥ���ʽ������A���ڼ���۲ͣ� B��ȥӰԺ����Ӱ�� C���������棻 D�����������
ÿλѧ�����ʾ�����ʱ����Ҫ��ֻѡ��������һ��ϲ���Ļ��ʽ����У��ί�ջ�ȫ���ʾ����ռ������������������Ƴ���ͼ��ʾ��ͳ��ͼ������ͳ��ͼ�ṩ����Ϣ������������⣺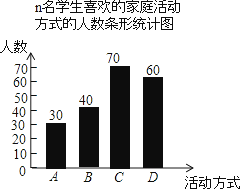
��1����n��ֵ��
��2�����ַ�ʽ������ѧ��ϲ���ķ�ʽΪ__����A��B��C��D���𣩣�ѡ����ַ�ʽ��ѧ������ռ�������ѧ�������İٷֱ�Ϊ_____����
��3������ͳ�ƽ�������Ƹ�У1800��ѧ����ϲ��C��ʽ��ѧ����ϲ��B��ʽ��ѧ�����������
���𰸡�
��1��
�⣺n=30+40+70+60=200��
��2��
�⣺��C��ѧ��������࣬
�����ַ�ʽ������ѧ��ϲ���ķ�ʽΪC��
![]() ��100%=35%��
��100%=35%��
�ʴ�Ϊ��C��35%��
��3��
�⣺1800��![]() =270���ˣ���
=270���ˣ���
�𣺸�У1800��ѧ����ϲ��C��ʽ��ѧ����ϲ��B��ʽ��ѧ���������Ϊ270�ˣ�
����������1����������ͼ����A��B��C��D�����������������ɽ��
��2��C��ѧ��������࣬��Ϊ���ַ�ʽ������ѧ��ϲ���ķ�ʽ����C�������������������ɵõ��ٷֱȣ�
��3���ֱ�����ϲ��C��ʽ��ѧ��������ϲ��B��ʽ��ѧ��������������ɽ��
�����㾫�����������⣬������Ҫ�˽�����ͳ��ͼ(������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯���)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O�����ߣ��е�ΪB������AO��AO���O���ڵ�C��BDΪ��O��ֱ��������CD������A=30�㣬��O�İ뾶Ϊ2����ͼ����Ӱ���ֵ����Ϊ��������
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC��D��BC���е㣬AC�Ĵ�ֱƽ���߷ֱ�AC��AD��AB�ڵ�E��O��F����ͼ��ȫ�������εĶ����ǣ�������
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��뾶ΪR��Բ�Ľ�Ϊn������������S����=![]() ���ɻ���l=
���ɻ���l=![]() ����S����=
����S����=![]() =
=![]()
![]() R=
R=![]() lR��ͨ���۲죬���Ƿ���S����=
lR��ͨ���۲죬���Ƿ���S����=![]() lR������S������=
lR������S������=![]() ���ס��ߣ�
���ס��ߣ�
������Σ�����̽���Ȼ�����ͼ�ڣ�����ͬ��ԲΧ�ɵ�Բ�������νصõ�һ���ֽ����Ȼ����������ʽ����Ӧ�ã�
��1�����Ȼ������ΪS�Ȼ� �� ![]() �ij�Ϊl1 ��
�ij�Ϊl1 �� ![]() �ij�Ϊl2 �� �߶�AD�ij�Ϊh��������ͬ��Բ�뾶R��r�IJ�����S����=
�ij�Ϊl2 �� �߶�AD�ij�Ϊh��������ͬ��Բ�뾶R��r�IJ�����S����=![]() �����ϵ�+�µף����ߣ��ú�l1 �� l2 �� h�Ĵ���ʽ��ʾS�Ȼ� �� ��֤����
�����ϵ�+�µף����ߣ��ú�l1 �� l2 �� h�Ĵ���ʽ��ʾS�Ȼ� �� ��֤����
��2����һ�γ�Ϊ40m�����Χ��һ����ͼ����ʾ���Ȼ��λ����߶�AD�ij�hΪ����ʱ�������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У���֪AD��AB���ڱ�AD��ȡ��E��ʹAE=AB������CE������E��EF��CE�����AB�����ӳ��߽��ڵ�F��
���룺��ͼ�٣�����F�ڱ�AB��ʱ���߶�AF��DE�Ĵ�С��ϵΪ______��
̽������ͼ�ڣ�����F�ڱ�AB���ӳ�����ʱ��EF���BC���ڵ�G���ж��߶�AF��DE�Ĵ�С��ϵ��������֤����
Ӧ�ã���ͼ�ڣ���AB=2��AD=5������̽���õ��Ľ��ۣ����߶�BG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬BD�ǡ�ABC��һ����ƽ���ߣ���O��E��F�ֱ���BD��BC��AC�ϣ����ı���OECF�������Σ�
��1����֤����O�ڡ�BAC��ƽ������;
��2����AC=5��BC=12����OE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�ǡ�����֮�ǡ���Ԯ�����ֳ�ͼ��С��ݴ˹����һ����ͼ2��ʾ����ѧģ�ͣ���֪��A��B��D������ͬһˮƽ���ϣ�CD��AD����A=30�㣬��CBD=75�㣬AB=60m��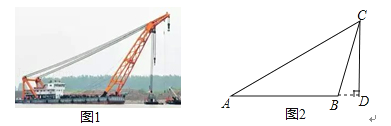
��1�����B��AC�ľ���.
��2�����߶�CD�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��ѵ�P����5��3������ƽ��8����λ�õ���P1 �� �ٽ���P1��ԭ����ת90��õ���P2 �� ���P2�������ǣ�������
A.��3����3��
B.����3��3��
C.��3��3����3����3��
D.��3����3����3��3��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com