
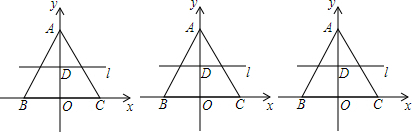
���� ��1������������ABC��������AB��OC�ij����ó���C�����ꣻ
��2����ͬʱ��ʼ����ʱ��t��ʾ��DQ=4-2t��PO=4-t�����s��t�ĺ�����ϵʽ��
��3�������MNPΪ����ֱ�������ε����������֣����õ�E����PQ�Ĵ�ֱƽ�����ϣ�Ҳ��ֱ��l�ϣ����ݹ��ɶ�����ƽ������ϵ����ֱ���ഹֱ������ϵ���Ļ�Ϊ-1�����t��D������꣮
��� �⣺��1����ABC�����=$\frac{1}{2}$BC•AO=32��
��BC=OA��
��BC=8��OC=OB=$\frac{1}{2}$BC=4��
�ʵ�C������Ϊ��0��4����
��2���������⻭��ͼ�Σ���ͼ1��ʾ��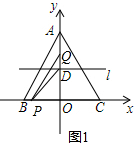
��BC=OA=8��
���P������Ϊ��t-4��0������Q�����꣨0��8-2t������D������Ϊ��0��4����
��DQ=4-2t��PO=4-t��
��PQD�����S=$\frac{1}{2}$DQ•PO=$\frac{1}{2}$����4-2t������4-t��=t2-6t+8��
�ߵ�Q���߶�AD�ϣ�
��DQ=4-2t��0����t��2��
�ʡ�PQD�����S����ʱ��t�Ĺ�ϵʽΪy=t2-6t+8��0��t��2����
��3��������ڣ����E������Ϊ��m��4����
�ɣ�2����֪��P������Ϊ��t-4��0������Q�����꣨0��8-2t����
��������ľ��빫ʽ�ɵã�PE=$\sqrt{��m-t+4��^{2}+{4}^{2}}$��EQ=$\sqrt{{m}^{2}+��4-8+2t��^{2}}$��PQ=$\sqrt{��t-4��^{2}+��-8+2t��^{2}}$��
��PQEΪ����ֱ�������η����������
��PE=EQ����PE2+EQ2=PQ2����E���߶�PQ�Ĵ�ֱƽ�����ϣ�
��PQ���е�M��$\frac{t-4}{2}$��4-t����
��ֱ��EQ�Ľ���ʽΪy=$\frac{1}{2}$x+8-2t��
�ߵ�M��ֱ��l�ϣ�
��y=4��
��$\frac{1}{2}$m+8-2t=4��
��m=-2-$\frac{3}{2}$t��
��EQ2+PE2=PQ2��
��2PE2=PQ2��
��2[��t-4-m��2+16]=5��t-4��2��
��t=-$\frac{4}{3}$���ᣩ��t=4����t=4ʱ����P��Q�غϣ�����ȥ����
�ڵ�PE=PQʱ����PE2+PQ2=EQ2��
��ֱ��PE�Ľ���ʽΪy=-$\frac{1}{2}$x+$\frac{1}{2}$��t-4����
�ߵ�E��ֱ��l�ϣ�
��-$\frac{1}{2}$m+$\frac{1}{2}$��t-4����
��m=t-4��
��10��t-4��2=m2+��4-2t��2��
��t=$\frac{16}{5}$��m=-$\frac{4}{5}$��t=8��m=0��
��E��-$\frac{4}{5}$��4����E��0��4����
�۵�QE=PQʱ����QE2+PQ2=PE2��
��ֱ��QE�Ľ���ʽΪy=$\frac{1}{2}$x+8-2t��
�ߵ�E��ֱ��l�ϣ�
��-$\frac{1}{2}$m+8-2t=4��
��m=8-4t��
��QE2+PQ2=PE2��
��10��t-4��2=��t-4-m��2+16��
��t=0��m=8��t=$\frac{8}{3}$��m=-$\frac{8}{3}$��
��E��$\frac{8}{3}$��4����E��-$\frac{8}{3}$��4����
����t=$\frac{16}{5}$��E��-$\frac{4}{5}$��4����t=8��E��0��4����t=0��E��$\frac{8}{3}$��4����t=$\frac{8}{3}$��E��-$\frac{8}{3}$��4����
���� ������һ�κ������ۺ��⣬���˶�ʱ���ʾ���߶κ͵�����꣬�������Ĺؼ�ʱ��������㣬������ѵ����Ե�EΪ����ֱ�������ε�ֱ�Ƕ���ʱ����PQ�Ĵ�ֱƽ���ߺ�ֱ��l�Ľ������E�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
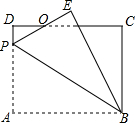 ��ͼ������ABCD�У�AB=8��BC=6��PΪAD��һ�㣬����ABP��BP��������EBP��PE��CD�ཻ�ڵ�O����OE=OD=1����AP�ij�Ϊ3.6��
��ͼ������ABCD�У�AB=8��BC=6��PΪAD��һ�㣬����ABP��BP��������EBP��PE��CD�ཻ�ڵ�O����OE=OD=1����AP�ij�Ϊ3.6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���۵���x��Ԫ/���� | �� | 20 | 30 | 40 | 50 | 60 | �� |
| ÿ����������y���� | �� | 500 | 400 | 300 | 200 | 100 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��AD��BC��AB��CD��BDƽ�֡�ABC��ͼ�����ADO��ȵĽǵĸ����ǣ�������
��ͼ��AD��BC��AB��CD��BDƽ�֡�ABC��ͼ�����ADO��ȵĽǵĸ����ǣ�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����O����ԭ��ΪԲ�ģ�2Ϊ�뾶��Բ����P��ֱ��y=-x+4�ϵ�һ�㣬����P����O��һ������PQ��QΪ�е㣬�����߳�PQ����СֵΪ2��
��ͼ����O����ԭ��ΪԲ�ģ�2Ϊ�뾶��Բ����P��ֱ��y=-x+4�ϵ�һ�㣬����P����O��һ������PQ��QΪ�е㣬�����߳�PQ����СֵΪ2���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com