练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图所示的图形中成轴对称的是（　　）
    分析：根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴，这时，我们也可以说这个图形关于这条直线（成轴）对称可得答案，
    解答：解：根据轴对称图形的定义可得C答案中5成轴对称，
    故选：C．
    点评：此题主要考查了轴对称，关键是掌握沿直线对折，直线两旁的部分能完全重合．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2012•岳阳）我们常见的炒菜锅和锅盖都是抛物线面，经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形，不妨简称为“锅线”，锅口直径为6dm，锅深3dm，锅盖高1dm（锅口直径与锅盖直径视为相同），建立直角坐标系如图①所示，如果把锅纵断面的抛物线记为C1，把锅盖纵断面的抛物线记为C2．
    （1）求C1和C2的解析式；
    （2）如图②，过点B作直线BE：y=
    1
    3
    x-1交C1于点E（-2，-
    5
    3
    ），连接OE、BC，在x轴上求一点P，使以点P、B、C为顶点的△PBC与△BOE相似，求出P点的坐标；
    （3）如果（2）中的直线BE保持不变，抛物线C1或C2上是否存在一点Q，使得△EBQ的面积最大？若存在，求出Q的坐标和△EBQ面积的最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：中考真题 题型：解答题

    我们常见的炒菜锅和锅盖都是抛物线面，经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形，不妨简称为“锅线”，锅口直径为6dm，锅深3dm，锅盖高1dm（锅口直径与锅盖直径视为相同），建立直接坐标系如图①所示，如果把锅纵断面的抛物线的记为C1，把锅盖纵断面的抛物线记为C2。
    （1）求C1和C2的解析式；
    （2）如图②，过点B作直线BE：y=x﹣1交C1于点E（﹣2，﹣），连接OE、BC，在x轴上求一点P，使以点P、B、C为顶点的△PBC与△BOE相似，求出P点的坐标；
    （3）如果（2）中的直线BE保持不变，抛物线C1或C2上是否存在一点Q，使得△EBQ的面积最大？若存在，求出Q的坐标和△EBQ面积的最大值；若不存在，请说明理由．

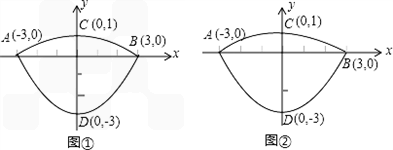
    查看答案和解析>>

    科目：初中数学 来源： 题型：

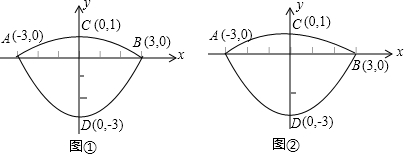
    我们常见的炒菜锅和锅盖都是抛物线面，经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形，不妨简称为“锅线”，锅口直径为6dm，锅深3dm，锅盖高1dm（锅口直径与锅盖直径视为相同），建立直接坐标系如图①所示，如果把锅纵断面的抛物线的记为C1，把锅盖纵断面的抛物线记为C2．

    （1）求C1和C2的解析式；

    （2）如图②，过点B作直线BE：y=x﹣1交C1于点E（﹣2，﹣），连接OE、BC，在x轴上求一点P，使以点P、B、C为顶点的△PBC与△BOE相似，求出P点的坐标；

    （3）如果（2）中的直线BE保持不变，抛物线C1或C2上是否存在一点Q，使得△EBQ的面积最大？若存在，求出Q的坐标和△EBQ面积的最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2012年初中毕业升学考试（湖南岳阳卷）数学（带解析） 题型：解答题

    我们常见的炒菜锅和锅盖都是抛物线面，经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形，不妨简称为“锅线”，锅口直径为6dm，锅深3dm，锅盖高1dm（锅口直径与锅盖直径视为相同），建立直接坐标系如图①所示，如果把锅纵断面的抛物线的记为C1，把锅盖纵断面的抛物线记为C2．
    （1）求C1和C2的解析式；
    （2）如图②，过点B作直线BE：y=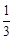x﹣1交C1于点E（﹣2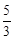，﹣），连接OE、BC，在x轴上求一点P，使以点P、B、C为顶点的△PBC与△BOE相似，求出P点的坐标；
    （3）如果（2）中的直线BE保持不变，抛物线C1或C2上是否存在一点Q，使得△EBQ的面积最大？若存在，求出Q的坐标和△EBQ面积的最大值；若不存在，请说明理由．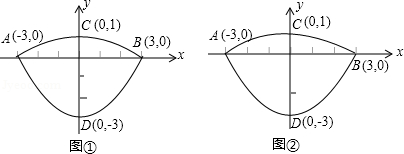

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图。

    （1）以A点为旋转中心，将△ABC绕点A顺时针旋转90°得，画出

    （2）作出△ABC关于坐标原点O成中心对称的

    （3）作出△ABC 关于y轴的轴对称图形

    查看答案和解析>>

    同步练习册答案