
分析 (1)根据有理数的加减法可以解答本题;
(2)根据有理数的乘除法可以解答本题;
(3)根据有理数的乘除法和减法可以解答本题;
(4)根据幂的乘方、有理数的乘除法和加法可以解答本题;
(5)根据乘法分配律可以解答本题;
(6)根据的幂的乘方、有理数的乘除法和减法可以解答本题.
解答 解:(1)4-(-28)+(-2)
=4+28+(-2)
=30;
(2)(-3)×[(-$\frac{2}{5}$)÷(-$\frac{1}{4}$)]
=(-3)×[$\frac{2}{5}×4$]
=(-3)×$\frac{8}{5}$
=-$\frac{24}{5}$;
(3)(-42)÷(-7)-(-6)×4
=6-(-24)
=6+24
=30;
(4)-32÷(-3)2+3×(-2)+|-4|
=-9÷9+(-6)+4
=-1+(-6)+4
=-3;
(5)(-24)×($\frac{3}{4}$-$\frac{5}{6}$+$\frac{7}{12}$)
=$(-24)×\frac{3}{4}-(-24)×\frac{5}{6}+(-24)×\frac{7}{12}$
=(-18)+20+(-14)
=-12;
(6)-14-(1-0.5)÷$\frac{5}{2}$×$\frac{1}{5}$
=-1-$\frac{1}{2}×\frac{2}{5}×\frac{1}{5}$
=-1-$\frac{1}{25}$
=-$\frac{26}{25}$.
点评 本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
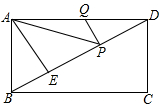 如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为3$\sqrt{3}$.
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
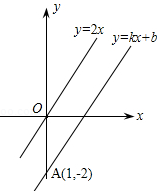 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点A(1,-2).
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点A(1,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
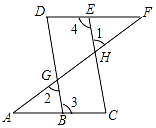 如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,求证:∠A=∠F
如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,求证:∠A=∠F 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com