
分析 (1)根据连续整数的乘积的倒数等于倒数差可得;
(2)利用(1)中所得规律裂项求解可得;
(3)根据$\frac{1}{2n(2n+2)}$=$\frac{1}{2}$($\frac{1}{2n}$-$\frac{1}{2n+2}$)裂项求和可得.
解答 解:(1)$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
故答案为:$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)①原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2011}$-$\frac{1}{2012}$=1-$\frac{1}{2012}$=$\frac{2011}{2012}$;
②原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$;
故答案为:$\frac{2011}{2012}$;$\frac{n}{n+1}$;
(3)原式=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+$\frac{1}{6}$-$\frac{1}{8}$+…+$\frac{1}{2010}$-$\frac{1}{2012}$)
=$\frac{1}{2}$×($\frac{1}{2}$-$\frac{1}{2012}$)
=$\frac{1}{2}$×$\frac{1005}{2012}$
=$\frac{1005}{4024}$,
故答案为:$\frac{1005}{4024}$.
点评 本题主要考查数字的变化规律,熟练掌握裂项求和的方法是解题的关键.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
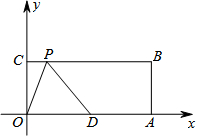 已知,如图:在平面直角坐标系中,O为坐标原点,OABC是长方形,点A、C的坐标分别为A(20,0),C(0,8),点D是OA的中点,点P在BC边上运动,△ODP是腰长为10的等腰三角形时,求满足条件的点P点坐标.
已知,如图:在平面直角坐标系中,O为坐标原点,OABC是长方形,点A、C的坐标分别为A(20,0),C(0,8),点D是OA的中点,点P在BC边上运动,△ODP是腰长为10的等腰三角形时,求满足条件的点P点坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com